Heat and Thermodynamics 6 Question 31
36. A solid body $X$ of heat capacity $C$ is kept in an atmosphere whose temperature is $T _A=300 K$. At time $t=0$, the temperature of $X$ is $T _0=400 K$. It cools according to Newton’s law of cooling. At time $t _1$ its temperature is found to be $350 K$. At this time $\left(t _1\right)$ the body $X$ is connected to a large body $Y$ at atmospheric temperature $T _A$ through a conducting rod of length $L$, cross-sectional area $A$ and thermal conductivity $K$. The heat capacity of $Y$ is so large that any variation in its temperature may be neglected. The cross-sectional area $A$ of the connecting rod is small compared to the surface area of $X$. Find the temperature of $X$ at time $t=3 t _1$.
(1998, 8M)
Show Answer
Answer:
Correct Answer: 36. $\left[300+12.5 e^{\frac{-2 K A t_1}{C L}}\right] \mathrm{K}$
Solution:
- In the first part of the question $\left(t \leq t _1\right)$
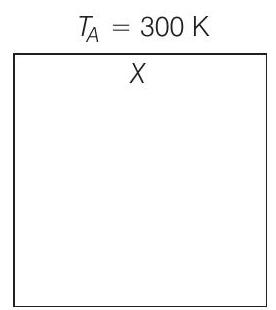
At $t=0, T _X=T _0=400 K$ and at $t=t _1, T _X=T _1=350 K$
Temperature of atmosphere, $T _A=300 K$ (constant)
This cools down according to Newton’s law of cooling. Therefore, rate of cooling $\propto$ temperature difference.
$$ \begin{array}{rlrl} & \therefore & \left(-\frac{d T}{d t}\right) & =k\left(T-T _A\right) \\ & \Rightarrow & \frac{d T}{T-T _A} & =-k d t \\ \Rightarrow & \int _{T _0}^{T _1} \frac{d T}{T-T _A} & =-k \int _0^{t _1} d t \\ \Rightarrow & & \ln \left(\frac{T _1-T _A}{T _0-T _A}\right) & =-k t _1 \end{array} $$
$$ \begin{array}{ll} \Rightarrow & k t _1=-\ln \left(\frac{350-300}{400-300}\right) \\ \Rightarrow & k t _1=\ln (2) \cdots(i) \end{array} $$
In the second part $\left(t>t _1\right)$, body $X$ cools by radiation (according to Newton’s law) as well as by conduction.
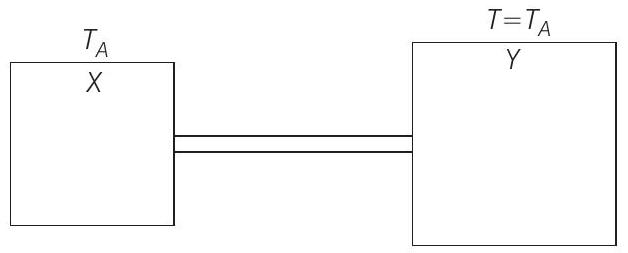
Therefore, rate of cooling
$=($ cooling by radiation $)+($ cooling by conduction $)$
$\therefore \quad\left(-\frac{d T}{d t}\right)=k\left(T-T _A\right)+\frac{K A}{C L}\left(T-T _A\right)\cdots(ii)$
In conduction, $\frac{d Q}{d t}=\frac{K A\left(T-T _A\right)}{L}=C\left(-\frac{d T}{d t}\right)$
$\therefore \quad\left(-\frac{d T}{d t}\right)=\frac{K A}{L C}\left(T-T _A\right)$
where, $C$ = heat capacity of body $X$
$$ \left(-\frac{d T}{d t}\right)=\left(k+\frac{K A}{C L}\right)\left(T-T _A\right)\cdots(iii) $$
Let at $t=3 t _1$, temperature of $X$ becomes $T _2$
Then from Eq. (iii)
$$ \begin{aligned} & \int _{T _1}^{T _2} \frac{d T}{T-T _A}=-\left(k+\frac{K A}{L C}\right) \int _{t _1}^{3 t _1} d t \\ & \ln \left(\frac{T _2-T _A}{T _1-T _A}\right)=-\left(k+\frac{K A}{L C}\right)\left(2 t _1\right) \\ & =-\left(2 k t _1+\frac{2 K A}{L C} t _1\right) \\ & \text { or } \ln \left(\frac{T _2-300}{350-300}\right)=-2 \ln (2)-\frac{2 K A t _1}{L C} \text {; } \\ & k t _1=\ln (2) \text { from Eq. (i). } \end{aligned} $$
This equation gives
$$ T _2=\left(300+12.5 e^{\frac{-2 K A t _1}{C L}}\right) K $$






