Heat and Thermodynamics 6 Question 27
32. The piston cylinder arrangement shown contains a diatomic gas at temperature $300 K$. The cross-sectional area of the cylinder is $1 m^{2}$. Initially the height of the piston above the base of the cylinder is $1 m$. The temperature is now raised to $400 K$ at constant pressure. Find the new height of the piston above the base of the cylinder.
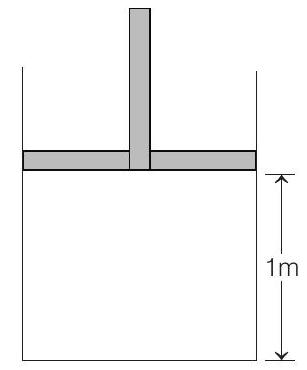
If the piston is now brought back to its original height without any heat loss, find the new equilibrium temperature of the gas. You can leave the answer in fraction. (2004, 2M)
Show Answer
Answer:
Correct Answer: 32. $\frac{4}{3} m , 448.8 K$
Solution:
- At constant pressure, $V \propto T$
$$ \begin{array}{ll} \text { or } & \frac{V _2}{V _1}=\frac{T _2}{T _1} \text { or } \frac{A h _2}{A h _1}=\frac{T _2}{T _1} \\ \therefore & h _2=h _1\left(\frac{T _2}{T _1}\right)=(1.0)\left(\frac{400}{300}\right) m=\frac{4}{3} m \end{array} $$
As there is no heat loss, process is adiabatic.
For adiabatic process,
$$ \begin{aligned} T _f V _f^{\gamma-1} & =T _i V _i^{\gamma-1} \\ \therefore \quad T _f & =T _i\left(\frac{V _i}{V _f}\right)^{\gamma-1}=(400)\left(\frac{h _i}{h _f}\right)^{1.4-1} \\ & =400\left(\frac{4}{3}\right)^{0.4}=448.8 K \end{aligned} $$






