Heat and Thermodynamics 6 Question 26
31. One end of a rod of length $L$ and cross-sectional area $A$ is kept in a furnace of temperature $T _1$. The other end of the rod is kept at a temperature $T _2$. The thermal conductivity of the material of the $\operatorname{rod}$ is $K$ and emissivity of the $\operatorname{rod}$ is $e$.
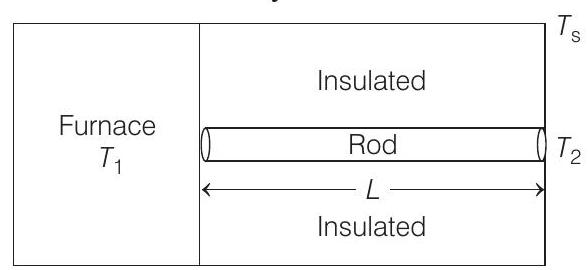
It is given that $T _2=T _s+\Delta T$, where $\Delta T«T _s, T _s$ being the temperature of the surroundings. If $\Delta T \propto\left(T _1-T _s\right)$, find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the $\operatorname{rod}$ is $T _2$.
(2004, 4M)
Show Answer
Answer:
Correct Answer: 31. Proportionality constant $=\frac{K}{4 e \sigma L T _s^{3}+K}$
Solution:
- Rate of heat conduction through rod $=$ rate of the heat lost from right end of the rod.
$\therefore \quad \frac{K A\left(T _1-T _2\right)}{L}=e A \sigma\left(T _2^{4}-T _s^{4}\right)\cdots(i)$
Given that
$$ \begin{aligned} T _2 & =T _s+\Delta T \\ T _2^{4} & =\left(T _s+\Delta T\right)^{4} \\ & =T _s^{4}\left(1+\frac{\Delta T}{T _s}\right)^{4} \end{aligned} $$
$$ \therefore \quad T _2^{4}=\left(T _s+\Delta T\right)^{4} $$
Using binomial expansion, we have
$$ \begin{aligned} T _2^{4} & =T _s^{4}\left(1+4 \frac{\Delta T}{T _s}\right) \quad\left(\text { as } \Delta T<T _s\right) \\ \therefore \quad T _2^{4}-T _s^{4} & =4(\Delta T)\left(T _s^{3}\right) \end{aligned} $$
Substituting in Eq. (i), we have
$$ \begin{array}{rlrl} & \frac{K\left(T _1-T _s-\Delta T\right)}{L} & =4 e \sigma T _s^{3} \cdot \Delta T \\ & \text { or } & \frac{K\left(T _1-T _s\right)}{L} & =\left(4 e \sigma T _s^{3}+\frac{K}{L}\right) \Delta T \\ & \therefore & \Delta T & =\frac{K\left(T _1-T _s\right)}{\left(4 e \sigma L T _s^{3}+K\right)} \end{array} $$
Comparing with the given relation, proportionality constant $=\frac{K}{4 e \sigma L T _s^{3}+K}$
