Heat and Thermodynamics 6 Question 16
20. The piston is taken completely out of the cylinder. The hole at the top is sealed. A water tank is brought below the cylinder and put in a position so that the water surface in the tank is at the same level as the top of the cylinder as shown in the figure. The density of the water is $\rho$. In equilibrium, the height $H$ of the water column in the cylinder satisfies
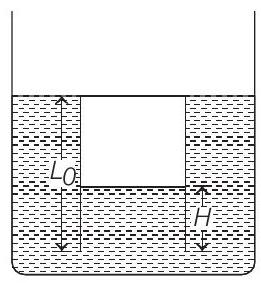
(2007, 4M)
(a) $\rho g\left(L _0-H\right)^{2}+p _0\left(L _0-H\right)+L _0 p _0=0$
(b) $\rho g\left(L _0-H\right)^{2}-p _0\left(L _0-H\right)-L _0 p _0=0$
(c) $\rho g\left(L _0-H\right)^{2}+p _0\left(L _0-H\right)-L _0 p _0=0$
(d) $\rho g\left(L _0-H\right)^{2}-p _0\left(L _0-H\right)+L _0 p _0=0$
Show Answer
Answer:
Correct Answer: 20. (c)
Solution:
$$ \begin{aligned} p _1 & =p _2 \\ p _0+\rho g\left(L _0-H\right) & =p \cdots(i) \end{aligned} $$
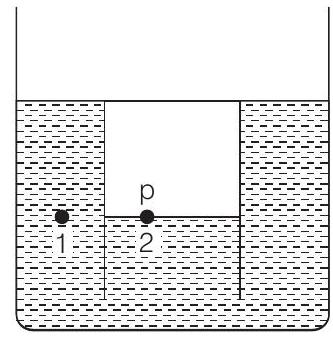
Now, applying $p _1 V _1=p _2 V _2$ for the air inside the cylinder, we have
$$ p _0\left(L _0\right)=p\left(L _0-H\right) $$
$$ \therefore \quad p=\frac{p _0 L _0}{L _0-H} $$
Substituting in Eq. (i), we have
$$ \begin{gathered} p _0+\rho g\left(L _0-H\right)=\frac{p _0 L _0}{L _0-H} \\ \text { or } \quad \rho g\left(L _0-H\right)^{2}+p _0\left(L _0-H\right)-p _0 L _0=0 \end{gathered} $$
$\therefore$ Correct option is (c).






