Heat and Thermodynamics 5 Question 56
57. Three moles of an ideal gas $\left(C _p=\frac{7}{2} R\right)$ at pressure, $p _A$ and temperature $T _A$ is isothermally expanded to twice its initial volume. It is then compressed at constant pressure to its original volume. Finally gas is compressed at constant volume to its original pressure $p _A$.
(1991, 4+4 M)
(a) Sketch $p-V$ and $p-T$ diagrams for the complete process.
(b) Calculate the net work done by the gas, and net heat supplied to the gas during the complete process.
Show Answer
Answer:
Correct Answer: 57. (a) $f=5$ (b) $W=1.23 p V$
Solution:
- (a) The $p-V$ and $p-T$ diagrams are shown below
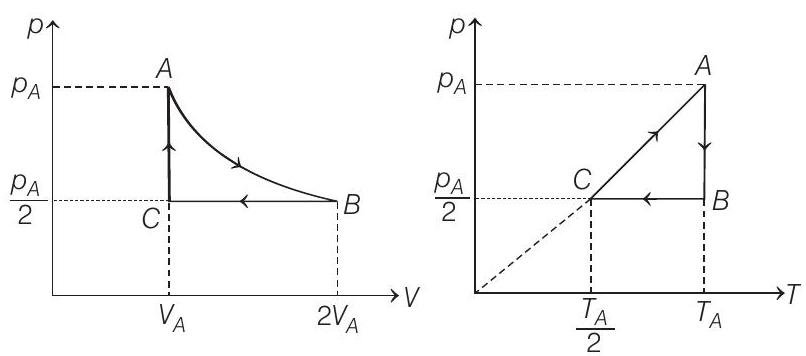
$$ (p V) _C=\frac{(p V) _A}{2} \Rightarrow \quad \therefore \quad T _C=\frac{T _A}{2} $$
(b) Process $\boldsymbol{A}-\boldsymbol{B} \quad T=$ constant
$\therefore \quad p \propto \frac{1}{V}, V$ is doubled. Therefore, $p$ will become half.
Further, $\quad V _A=\frac{n R T _A}{p _A}=\frac{3 R T _A}{p _A}$
$$ \begin{gathered} \Delta U _{A B}=0 \\ \therefore Q _{A B}=W _{A B}=n R T _A \ln \left(\frac{2 V _A}{V _A}\right) \\ =3 R T _A \ln (2)=2.08 R T _A \end{gathered} $$
Process $B$ - $C$
$Q _{B C}=n C _p\left(T _C-T _B\right)$
$$ \begin{aligned} & =(3)\left(\frac{7}{2} R\right)\left(\frac{T _A}{2}-T _A\right)=-\frac{21}{4} R T _A \\ & =-5.25 R T _A \end{aligned} $$
Process $\boldsymbol{C}-\boldsymbol{A} V=$ constant
$$ \begin{aligned} \therefore \quad W _{C A} & =0 \\ \text { or } \quad Q _{C A} & =\Delta U _{C A}=n C _V\left(T _A-T _C\right) \\ & =(3)\left(\frac{5}{2} R\right)\left(T _A-\frac{T _A}{2}\right)=3.75 R T _A \end{aligned} $$
In a cyclic process,
$$ \begin{aligned} \Delta U & =0 \\ \therefore \quad Q _{\text {net }} & =W _{\text {net }}=0.58 R T _A \end{aligned} $$






