Heat and Thermodynamics 5 Question 51
52. One mole of a diatomic ideal gas $(\gamma=1.4)$ is taken through a cyclic process starting from point $A$. The process $A \rightarrow B$ is an adiabatic compression. $B \rightarrow C$ is isobaric expansion, $C \rightarrow D$ an adiabatic expansion and $D \rightarrow A$ is isochoric. The volume ratio are $V _A / V _B=16$ and $V _C / V _B=2$ and the temperature at $A$ is $T _A=300 K$. Calculate the temperature of the gas at the points $B$ and $D$ and find the efficiency of the cycle.
$(1997,5 M)$
Show Answer
Answer:
Correct Answer: 52. $T _B=909 K, T _D=791.4 K, 61.4 \%$
Solution:
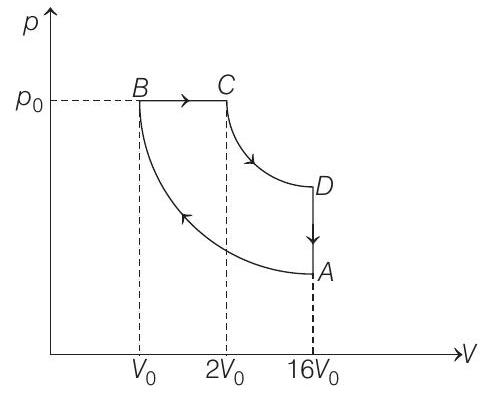
- The corresponding $p$ - $V$ diagram is as shown
Given $T _A=300 K, n=1, \gamma=1.4, V _A / V _B=16$ and $V _C / V _B=2$
Let $\quad V _B=V _0$ and $p _B=p _0$
Then, $\quad V _C=2 V _0$ and $V _A=16 V _0$
Temperature at $B$
Process $A-B$ is adiabatic.
Hence, $\quad T _A V _A^{\gamma-1}=T _B V _B^{\gamma-1}$
or
$$ \begin{aligned} T _B & =T _A\left(\frac{V _A}{V _B}\right)^{\gamma-1}=(300)(16)^{1.4-1} \\ T _B & =909 K \end{aligned} $$
Temperature at $D$
$B \rightarrow C$ is an isobaric process ( $p=$ constant)
$$ \begin{aligned} & \therefore \quad T \propto V, V _C=2 V _B \\ & \therefore \quad T _C=2 T _B=(2)(909) K \\ & T _C=1818 K \end{aligned} $$
Now, the process $C \rightarrow D$ is adiabatic.
Therefore, $\quad T _D=T _C\left(\frac{V _C}{V _D}\right)^{\gamma-1}=(1818)\left(\frac{2}{16}\right)^{1.4-1}$
$$ T _D=791.4 K $$
Efficiency of cycle
Efficiency of cycle (in percentage) is defined as
$$ \eta=\frac{\text { Net work done in the cycle }}{\text { Heat absorbed in the cycle }} \times 100 $$
or
$$ \begin{aligned} \eta & =\frac{W _{\text {Total }}}{Q _{+ve}} \times 100 \\ & =\frac{Q _{+ve}-Q _{-ve}}{Q _{+ve}} \times 100=\left(1-\frac{Q _1}{Q _2}\right) \times 100 \end{aligned} $$
where, $Q _1=$ negative heat in the cycle (heat released) and
$Q _2=$ positive heat in the cycle (heat absorbed) In the cycle
In the cycle
$$ \begin{aligned} & Q _{A B}=Q _{C D}=0 (Adiabatic process)\\ & Q _{D A}=n C _V \Delta T=(1)\left(\frac{5}{2} R\right)\left(T _A-T _D\right) \\ & \qquad\left(C _V=\frac{5}{2} R\right. \text { for a diatomic gas) } \\ & = \\ & =\frac{5}{2} \times 8.31(300-791.4) J \end{aligned} $$
or $\quad Q _{D A}=-10208.8 J$
and $\quad Q _{B C}=n C _p \Delta T=(1)\left(\frac{7}{2} R\right)\left(T _C-T _B\right)$
$\left(C _p=\frac{7}{2} R\right.$ for a diatomic gas)
$$ =\left(\frac{7}{2}\right)(8.31)(1818-909) J $$
or $\quad Q _{B C}=26438.3 J$
Therefore, substituting $Q _1=10208.8 J$ and $Q _2=26438.3 J$ in Eq. (i), we get
$\therefore \quad \eta={1-\frac{10208.8}{26438.3} } \times 100$ or $\eta=61.4 \%$






