Heat and Thermodynamics 5 Question 49
50. One mole of an ideal monoatomic gas is taken round the cyclic process $A B C A$ as shown in figure. Calculate
$(1998,8 M)$
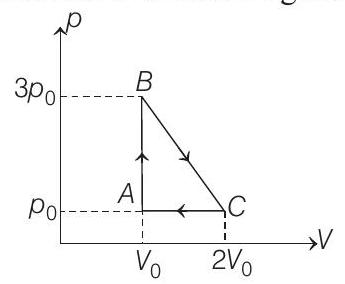
(a) the work done by the gas.
(b) the heat rejected by the gas in the path $C A$ and the heat absorbed by the gas in the path $A B$.
(c) the net heat absorbed by the gas in the path $B C$.
(d) the maximum temperature attained by the gas during the cycle.
Show Answer
Answer:
Correct Answer: 50. (a) $p _0 V _0$ (b) $\frac{5}{2} p _0 V _0, 3 p _0 V _0$ (c) $\frac{p _0 V _0}{2}$ (d) $\frac{25}{8} \frac{p _0 V _0}{R}$
Solution:
- (a) $A B C A$ is a clockwise cyclic process.
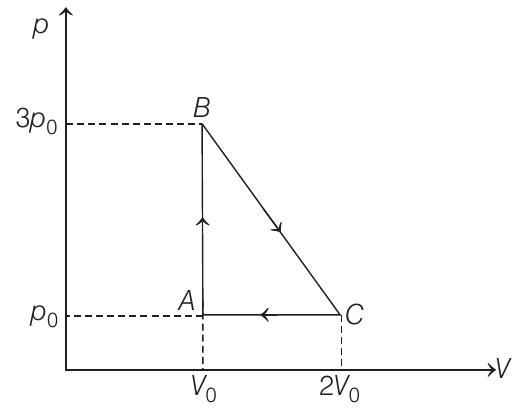
$\therefore$ Work done by the gas
$W=+$ Area of triangle $A B C$
$$ =\frac{1}{2}(\text { base })(\text { height })=\frac{1}{2}\left(2 V _0-V _0\right)\left(3 p _0-p _0\right) $$
$$ W=p _0 V _0 $$
(b) Number of moles $n=1$ and gas is monoatomic, therefore
$$ \begin{aligned} C _V & =\frac{3}{2} R \quad \text { and } \quad C _p & =\frac{5}{2} R \\ \Rightarrow \quad \frac{C _V}{R} & =\frac{3}{2} \quad \text { and } \quad \frac{C _p}{R} & =\frac{5}{2} \end{aligned} $$
(i) Heat rejected in path $\boldsymbol{C A}$ (Process is isobaric)
$\therefore d Q _{C A}=C _p d T=C _p\left(T _f-T _i\right)$
$$ =C _p\left(\frac{p _f V _f}{R}-\frac{p _i V _i}{R}\right)=\frac{C _p}{R}\left(p _f V _f-p _i V _i\right) $$
Substituting the values
$$ d Q _{C A}=\frac{5}{2}\left(p _0 V _0-2 p _0 V _0\right)=-\frac{5}{2} p _0 V _0 $$
Therefore, heat rejected in the process $C A$ is $\frac{5}{2} p _0 V _0$.
(ii) Heat absorbed in path $\boldsymbol{A B}$ (Process is isochoric)
$\therefore d Q _{A B}=C _V d T=C _V\left(T _f-T _i\right)$
$$ \begin{aligned} & =C _V\left(\frac{p _f V _f}{R}-\frac{p _i V _i}{R}\right) \\ & =\frac{C _V}{R}\left(p _f V _f-p _i V _i\right) \\ & =\frac{3}{2}\left(p _f V _f-p _i V _i\right) \\ & =\frac{3}{2}\left(3 p _0 V _0-p _0 V _0\right) \\ d Q _{A B} & =3 p _0 V _0 \end{aligned} $$
$\therefore$ Heat absorbed in the process $A B$ is $3 p _0 V _0$.
(c) Let $d Q _{B C}$ be the heat absorbed in the process $B C$ : Total heat absorbed,
$$ \begin{aligned} & d Q=d Q _{C A}+d Q _{A B}+d Q _{B C} \\ & d Q=\left(-\frac{5}{2} p _0 V _0\right)+\left(3 p _0 V _0\right)+d Q _{B C} \\ & d Q=d Q _{B C}+\frac{p _0 V _0}{2} \end{aligned} $$
Change in internal energy, $d U=0$
$$ \begin{aligned} & \therefore \quad d Q=d W \\ & \therefore \quad d Q _{B C}+\frac{p _0 V _0}{2}=p _0 V _0 \therefore d Q _{B C}=\frac{p _0 V _0}{2} \\ & \therefore \text { Heat absorbed in the process } B C \text { is } \frac{p _0 V _0}{2} . \end{aligned} $$
(d) Maximum temperature of the gas will be somewhere between $B$ and $C$. Line $B C$ is a straight line. Therefore, $p$ - $V$ equation for the process $B C$ can be written as
$$ \begin{aligned} p & =-m V+c \quad (y=m x+c)\\ \text { Here, } \quad m & =\frac{2 p _0}{V _0} \quad \text { and } \quad c=5 p _0 \\ \therefore \quad p & =-\left(\frac{2 p _0}{V _0}\right) V+5 p _0 \end{aligned} $$
Multiplying the equation by $V$,
$$ \begin{aligned} p V & =-\left(\frac{2 p _0}{V _0}\right) V^{2}+5 p _0 V \quad(p V=R T \text { for } n=1) \\ R T & =-\left(\frac{2 p _0}{V _0}\right) V^{2}+5 p _0 V \\ \text { or } T & =\frac{1}{R}\left[5 p _0 V-\frac{2 p _0}{V _0} V^{2}\right] \cdots(i) \end{aligned} $$
For $T$ to be maximum, $\frac{d T}{d V}=0$
$\Rightarrow \quad 5 p _0-\frac{4 p _0}{V _0} V=0 \Rightarrow V=\frac{5 V _0}{4}$
i.e. at $V=\frac{5 V _0}{4}$, (on line $B C$ ), temperature of the gas is maximum. From Eq. (i) this maximum temperature will be
$$ \begin{aligned} T _{\max } & =\frac{1}{R}\left[5 p _0\left(\frac{5 V _0}{4}\right)-\frac{2 p _0}{V _0}\left(\frac{5 V _0}{4}\right)^{2}\right] \\ T _{\max } & =\frac{25}{8} \frac{p _0 V _0}{R} \end{aligned} $$






