Heat and Thermodynamics 4 Question 10
11. A vertical closed cylinder is separated into two parts by a frictionless piston of mass $m$ and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is $l _1$ and that below the piston is $l _2$, such that $l _1>l _2$. Each part of the cylinder contains $n$ moles of an ideal gas at equal temperature $T$. If the piston is stationary, its mass $m$, will be given by
(where, $R$ is universal gas constant and $g$ is the acceleration due to gravity)
(2019 Main019, 12 Jan II)
(a) $\frac{n R T}{g}\left[\frac{l _1-l _2}{l _1 l _2}\right]$
(b) $\frac{n R T}{g}\left[\frac{1}{l _2}+\frac{1}{l _1}\right]$
(c) $\frac{R T}{g}\left[\frac{2 l _1+l _2}{l _1 l _2}\right]$
(d) $\frac{R T}{n g}\left[\frac{l _1-3 l _2}{l _1 l _2}\right]$
Show Answer
Answer:
Correct Answer: 11. (a)
Solution:
- Key Idea
As piston is in equilibrium, so net force on piston is zero.
When the piston is stationary, i.e. on equilibrium as shown in the figure below,
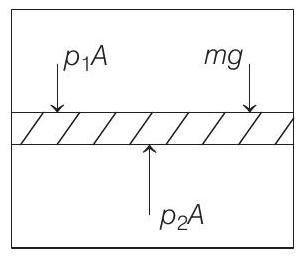
$$ \begin{aligned} & \text { then } \quad p _1 A+m g=p _2 A \\ & \Rightarrow \quad m g=p _2 A-p _1 A \\ & \text { or } \quad m g=\left(\frac{n R T A}{V _2}-\frac{n R T A}{V _1}\right) \\ & {\because p V=n R T \text { (ideal gas equation) }} \\ & =n R T\left(\frac{A}{A l _2}-\frac{A}{A l _1}\right)=n R T\left(\frac{l _1-l _2}{l _1 l _2}\right) \\ & \text { or } \quad m=\frac{n R T}{g}\left(\frac{l _1-l _2}{l _1 l _2}\right) \end{aligned} $$






