Heat and Thermodynamics 3 Question 4
4. Temperature difference of $120^{\circ} C$ is maintained between two ends of a uniform $\operatorname{rod} A B$ of length $2 L$. Another bent $\operatorname{rod} P Q$, of same cross-section as $A B$ and length $\frac{3 L}{2}$ is connected across $A B$ (see figure). In steady state, temperature difference between $P$ and $Q$ will be close to
(2019 Main, 9 Jan I)
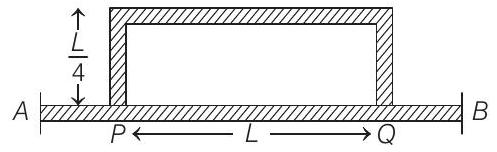
(a) $45^{\circ}$
(b) $35^{\circ} C$
(c) $75^{\circ} C$
(d) $60^{\circ} C$
Show Answer
Answer:
Correct Answer: 4. (a)
Solution:
- According to the given question, the given figure with its length for each section is given as below
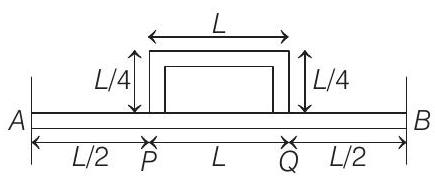
The above figure considering that every section has the same thermal conductivity, then in terms of thermal resistance is shown in the figure below,
Net resistance of the section $P Q R S$ is $=\frac{R \times \frac{3 R}{2}}{\frac{5 R}{2}}=\frac{3 R}{5}\cdots(i)$
Total resistance of the net network, $R _{\text {net }}$
$$ =\frac{R}{2}+\frac{R}{2}+\frac{3 R}{5}=\frac{8 R}{5} $$
$\therefore$ Thermal current, $I=\frac{\Delta T _{A B}}{R _{\text {net }}}$
$$ I=\frac{120-0}{\left(\frac{8 R}{5}\right)}=\frac{120 \times 5}{8 R} $$
Thus, the net temperature difference between point $P$ and $Q$ is
$$ \begin{aligned} T _P-T _Q & =I \times \frac{3 R}{5} [Using \quad eq. (i)]\\ & =\frac{120 \times 5}{8 R} \times \frac{3 R}{5}=45^{\circ} C \end{aligned} $$






