Heat and Thermodynamics 3 Question 24
24. A composite block is made of slabs $A, B, C, D$ and $E$ of different thermal conductivities (given in terms of a constant $K)$ and sizes (given in terms of length, $L$ ) as shown in the figure. All slabs are of same width. Heat $Q$ flows only from left to right through the blocks. Then, in steady state (2011)
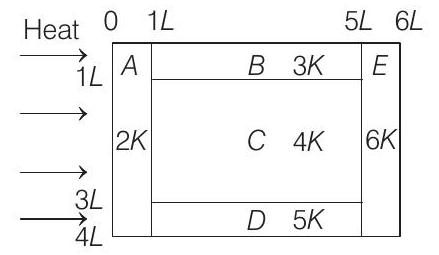
(a) heat flow through $A$ and $E$ slabs are same
(b) heat flow through slab $E$ is maximum
(c) temperature difference across slab $E$ is smallest
(d) heat flow through $C$ = heat flow through $B+$ heat flow through $D$
Show Answer
Answer:
Correct Answer: 24. (a,c,d)
Solution:
- Thermal resistance $R=\frac{l}{K A}$
$$ \begin{aligned} & R _A=\frac{L}{(2 K)(4 L w)} \quad(\text { Here } w=\text { width) } \\ &=\frac{1}{8 K w}, \\ & R _B=\frac{4 L}{3 K(L w)}=\frac{4}{3 K w} \\ & R _C=\frac{4 L}{(4 K)(2 L w)}=\frac{1}{2 K w} \\ & R _D=\frac{4 L}{(5 K)(L w)}=\frac{4}{5 K w} \\ & R _E=\frac{L}{(6 K)(L w)}=\frac{1}{6 K w} \\ & R _A: R _B: R _C: R _D: R _E \\ &=15: 160: 60: 96: 12 \end{aligned} $$
So, let us write, $R _A=15 R, R _B=160 R$ etc and draw a simple electrical circuit as shown in figure
$H=$ Heat current $=$ Rate of heat flow.
$$ H _A=H _E=H $$
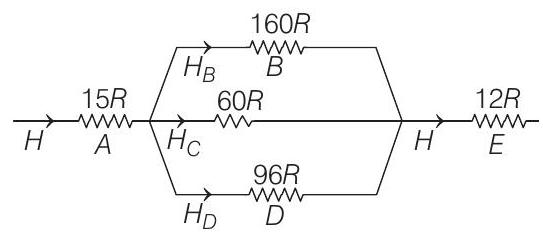
In parallel current distributes in inverse ratio of resistance.
$\therefore H _B: H _C: H _D=\frac{1}{R _B}: \frac{1}{R _C}: \frac{1}{R _D}$
$$ \begin{gathered} =\frac{1}{160}: \frac{1}{60}: \frac{1}{96} \\ =9: 24: 15 \\ \therefore \quad H _B=\left(\frac{9}{9+24+15}\right) H=\frac{3}{16} H \\ H _C=\left(\frac{24}{9+24+15}\right) H=\frac{1}{2} H \end{gathered} $$
and $\quad H _D=\left(\frac{15}{9+24+15}\right) H=\frac{5}{16} H$
$$ H _C=H _B+H _D $$
Temperature difference (let us call it $T$ )
$=($ Heat current $) \times($ Thermal resistance $)$
$T _A=H _A R _A=(H)(15 R)=15 H R$
$T _B=H _B R _B=\left(\frac{3}{16} H\right)(160 R)=30 H R$
$T _C=H _C R _C=\left(\frac{1}{2} H\right)(60 R)=30 H R$
$T _D=H _D R _D=\left(\frac{5}{16} H\right)(96 R)=30 H R$
$T _E=H _E R _E=(H)(12 R)=12 H R$
Here, $T _E$ is minimum. Therefore option (c) is also correct.
$\therefore$ Correct options are (a), (c) and (d).
