Heat and Thermodynamics 3 Question 18
18. A black body is at a temperature of $2880 K$. The energy of radiation emitted by this body with wavelength between $499 nm$ and $500 nm$ is $U _1$, between $999 nm$ and $1000 nm$ is $U _2$ and between $1499 nm$ and $1500 nm$ is $U _3$. The Wien constant, $b=2.88 \times 10^{6} nm-K$. Then,
(1998, 2M)
(a) $U _1=0$
(b) $U _3=0$
(c) $U _1>U _2$
(d) $U _2>U _1$
Show Answer
Answer:
Correct Answer: 18. (d)
Solution:
- Wien’s displacement law is
$$ \begin{aligned} & \lambda _m T & =b \quad(b=\text { Wien’s constant }) \\ \therefore & \lambda _m & =\frac{b}{T}=\frac{2.88 \times 10^{6} nm-K}{2880 K} \\ \therefore & \lambda & =1000 nm \end{aligned} $$
Energy distribution with wavelength will be as follows :
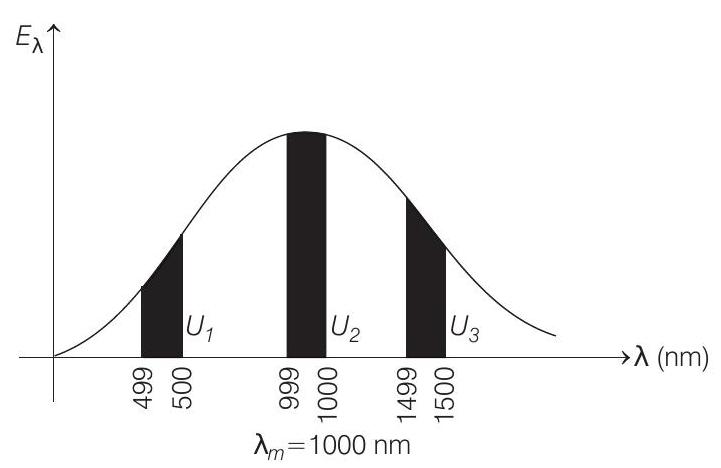
From the graph it is clear that
$$ U _2>U _1 \quad \text { (In fact } U _2 \text { is maximum) } $$






