Gravitation 5 Question 9
10. Three particles, each of mass $m$, are situated at the vertices of an equilateral triangle of side length $a$. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation $a$. Find the initial velocity that should be given to each particle and also the time period of the circular motion.
$(1988,5 M)$
Show Answer
Answer:
Correct Answer: 10. $v=\sqrt{\frac{G m}{a}}, T=2 \pi \sqrt{\frac{a^{3}}{3 G m}}$
Solution:
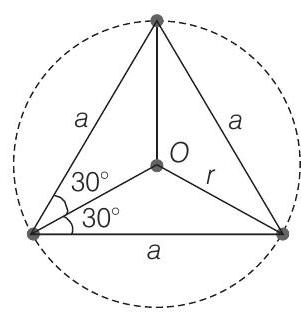
- Centre should be at $O$ and radius $r$.
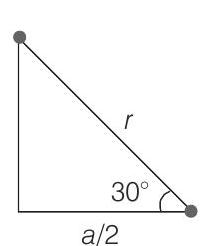
We can calculate $r$ from figure (b).
$$ \frac{a / 2}{r}=\cos 30^{\circ}=\frac{\sqrt{3}}{2} \Rightarrow \therefore \quad r=\frac{a}{\sqrt{3}} $$
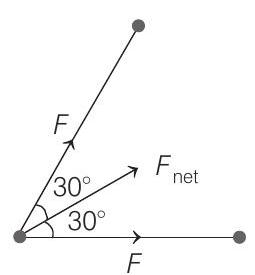
Further net force on any particle towards centre
(a)
(b)
(c)
$$ \begin{aligned} F_{\text {net }} & =2 F \cos 30^{\circ}=2 \frac{G m^{2}}{a^{2}} \frac{\sqrt{3}}{2} \\ & =\frac{\sqrt{3} G m^{2}}{a^{2}} \end{aligned} $$
This net force should be equal to $\frac{m v^{2}}{r}$
$\therefore \frac{\sqrt{3} G m^{2}}{a^{2}}=\frac{m v^{2}}{a / \sqrt{3}}$
$\Rightarrow \quad v=\sqrt{\frac{G m}{a}}$ Time period of circular motion
$$ T=\frac{2 \pi r}{v}=\frac{2 \pi(a / \sqrt{3})}{\sqrt{G m / a}}=2 \pi \sqrt{\frac{a^{3}}{3 G m}} $$






