Gravitation 2 Question 4
7. A spherically symmetric gravitational system of particles has a mass density $\rho=\begin{gathered}\rho_{0} \text { for } r \leq R \ 0 \text { for } r>R\end{gathered}$, where $\rho_{0}$ is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed $v$ as a function of distance $r$ from the centre of the system is represented by
(a)
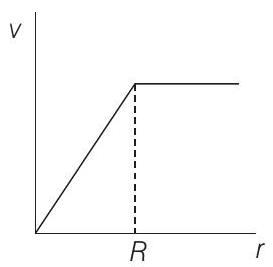
(b)
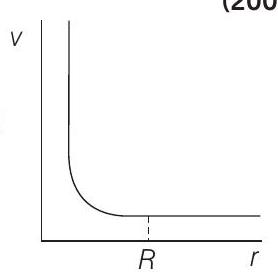
(c)
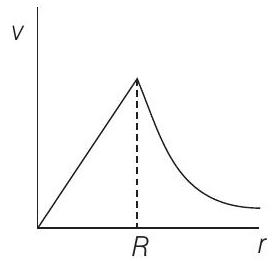
(d)
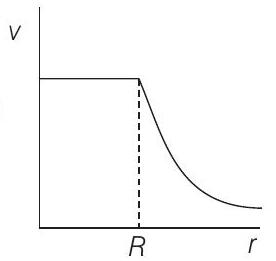
Show Answer
Answer:
Correct Answer: 7. (c)
Solution:
- For $r \leq R, \frac{m v^{2}}{r}=\frac{G m M}{r^{2}}$
Here,
$$ M=\frac{4}{3} \pi r^{3} \rho_{0} $$
Substituting in Eq. (i), we get $v \propto r$
i.e. $v-r$ graph is a straight line passing through origin.
For $r>R$,
$$ \frac{m v^{2}}{r}=\frac{G m \frac{4}{3} \pi R^{3} \rho_{0}}{r^{2}} \text { or } v \propto \frac{1}{\sqrt{r}} $$
The corresponding $v-r$ graph will be as shown in option (c).
