Gravitation 2 Question 11
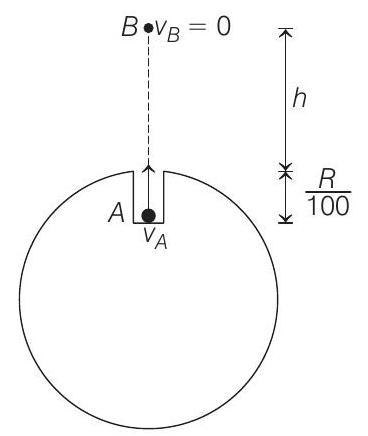
15. There is a crater of depth $\frac{R}{100}$ on the surface of the moon (radius $R$ ). A projectile is fired vertically upward from the crater with velocity, which is equal to the escape velocity $v$ from the surface of the moon. Find the maximum height attained by the projectile that the satellite could escape from the gravitational field of earth is
$(2003,4 \mathrm{M})$
(2019 Main, 11 Jan II)
(a) $\sqrt{\frac{g R}{2}}$
(b) $\sqrt{g R}$
(c) $\sqrt{2 g R}$
(d) $\sqrt{g R}(\sqrt{2}-1)$
Show Answer
Answer:
Correct Answer: 15. 99.5 R
Solution:
- Speed of particle at $A, v_{A}$
= escape velocity on the surface of earth $=\sqrt{\frac{2 G M}{R}}$
At highest point $B, v_{B}=0$
Applying conservation of mechanical energy, decrease in kinetic energy $=$ increase in gravitational potential energy
or $\quad \frac{1}{2} m v_{A}^{2}=U_{B}-U_{A}=m\left(v_{B}-v_{A}\right)$
or $\quad \frac{v_{A}^{2}}{2}=v_{B}-v_{A}$
$\therefore \frac{G M}{R}=-\frac{G M}{R+h}–\frac{G M}{R^{3}} 1.5 R^{2}-0.5 R-\frac{R}{100}^{2}$
or $\frac{1}{R}=-\frac{1}{R+h}+\frac{3}{2 R}-\frac{1}{2} \frac{99}{100}^{2} \cdot \frac{1}{R}$
Solving this equation, we get
$$ h=99.5 R $$
