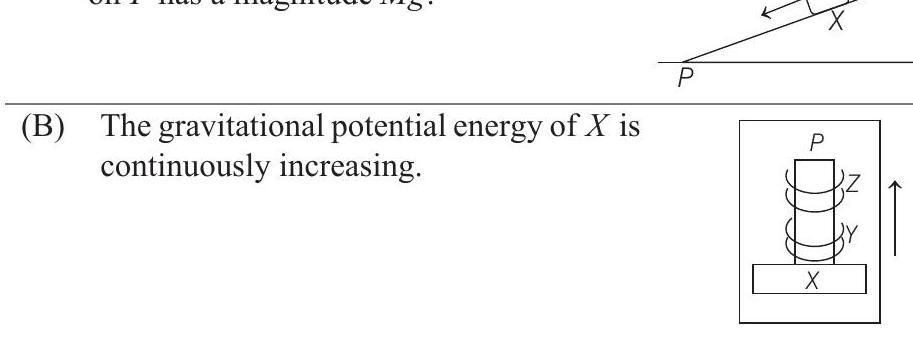Question 10
- Column II shows five systems in which two objects are labelled as and . Also in each case a point is shown. Column I gives some statements about and/or . Match these statements to the appropriate system(s) from Column II
(2009)
Column I
(A) The force exerted by on has a magnitude .
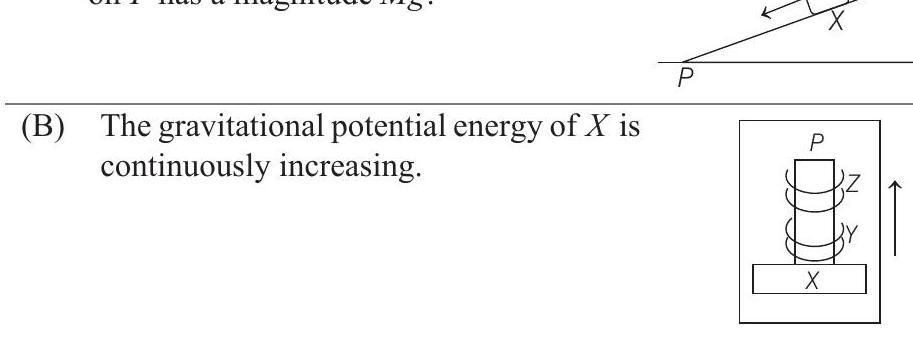
Column II
(p) Block of mass left on a fixed inclined plane , slides on it with a constant velocity.
(q) Two ring magnets and , each of mass , are kept in frictionless vertical plastic stand so that they repel each other. rests on the base and hangs in air in equilibrium. is the topmost point of the stand on the common axis of the two rings. The whole system is in a lift that is going up with a constant velocity.
(C) Mechanical energy of the system is continuously decreasing.
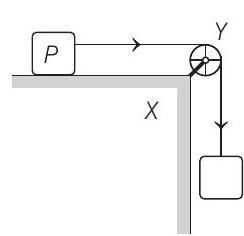
(r) A pulley of mass is fixed to a table through a clamp . A block of mass hangs from a string that goes over the pulley and is fixed at point of the table. The whole system is kept in a lift that is going down with a constant velocity.
(D) The torque of the weight of about point is zero.
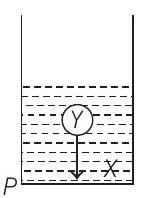
(s) A sphere of mass is put in a non-viscous liquid kept in a container at rest. The sphere is released and it moves down in the liquid.
(t) A sphere of mass is falling with its terminal velocity in a viscous liquid kept in a container.
Show Answer
Answer:
Correct Answer: 11. ,
B-q, s, t,
Solution:
- (p) Constant velocity means, net acceleration or net force .
Net force exerted by and in upward direction (opposite to its weight ). Since is moving with constant velocity, some friction is there between and .
Therefore, some work is done against friction and mechanical energy of is continuously decreasing.
(s) Potential energy of is decreasing but same volume of rises up. Hence, potential energy of is increasing. Some part of mechanical energy of is lost in the form of heat in doing work against viscous forces. Net force on in this case is downwards before attains its terminal velocity.
(t) After attaining the terminal velocity, net force on becomes zero. Hence, force on from is , upwards. Rest of the logics are same as discussed in part (s).