Electrostatics 7 Question 5
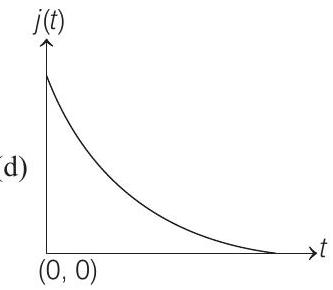
5. An infinite line charge of uniform electric charge density $\lambda$ lies along the axis of an electrically conducting infinite cylindrical shell of radius $R$. At time $t=0$, the space inside the cylinder is filled with a material of permittivity $\varepsilon$ and electrical conductivity $\sigma$. The electrical conduction in the material follows Ohm’s law. Which one of the following graphs best describes the subsequent variation of the magnitude of current density $j(\mathrm{t})$ at any point in the material?
(a)
(b)
(c)
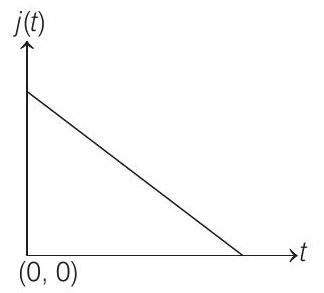
(d)
Show Answer
Answer:
Correct Answer: 5. (d)
Solution:
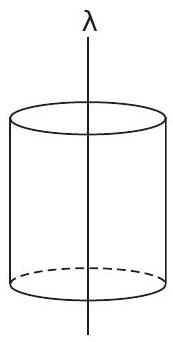
Suppose charger per unit length at any instant is $\lambda$
Initial value of $\lambda$ is suppose $\lambda_{0}$.
Electric field at a distance $r$ at any instant is
$$ \begin{aligned} E & =\frac{\lambda}{2 \pi \varepsilon r} \\ J & =\sigma E=\sigma \frac{\lambda}{2 \pi \varepsilon r} \\ i & =\frac{d q}{d t}=J(A)=-J \sigma 2 \pi r l \\ \frac{d \lambda l}{d t} & =-\frac{\lambda}{2 \pi \varepsilon r} \times \sigma 2 \pi r l \\ { }^{\lambda} d \lambda & =-\frac{\sigma}{\varepsilon} \int_{a}^{t} d t \end{aligned} $$
$$ \begin{aligned} \Rightarrow \quad \lambda & =\lambda_{0} e^{-\frac{\alpha}{\varepsilon} t} \\ J & =\frac{\sigma}{2 \pi \varepsilon r} \lambda=\frac{\sigma \lambda_{0}}{2 \pi \varepsilon r} e^{-\frac{\sigma}{\varepsilon} t}=J_{0} e^{-\frac{\sigma}{\varepsilon} t} \\ \text { Here, } \quad J_{0} & =\frac{\sigma \lambda_{0}}{2 \pi \varepsilon r} \end{aligned} $$
$\therefore J(t)$ decreases exponentially as shown in figure below.