Electrostatics 7 Question 29
31. A non-conducting disc of radius $a$ and uniform positive surface charge density $\sigma$ is placed on the ground with its axis vertical. A particle of mass $m$ and positive charge $q$ is dropped, along the axis of the disc from a height $H$ with zero initial velocity. The particle has $q / m=4 \varepsilon_{0} g / \sigma$. (1999, 10M)
(a) Find the value of $H$ if the particle just reaches the disc.
(b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.
Show Answer
Answer:
Correct Answer: 31. (a) $H=\frac{4}{3} a$
(b) $H=\frac{a}{\sqrt{3}}$
Solution:
- Potential at a height $\boldsymbol{H}$ on the axis of the disc $\boldsymbol{V}(\boldsymbol{P})$
The charge $d q$ contained in the ring shown in figure
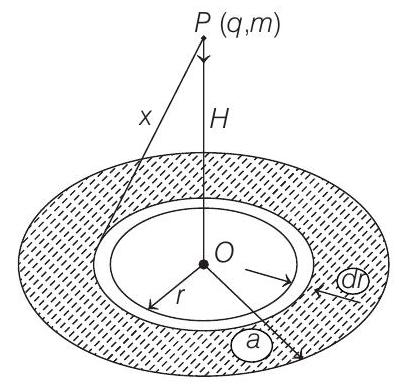
$$ d q=(2 \pi r d r) \sigma $$
Potential at $P$ due to this ring
$$ \begin{aligned} & d V=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{d q}{x} \text { where } x=\sqrt{H^{2}+r^{2}} \\ & d V=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{(2 \pi r d r) \sigma}{\sqrt{H^{2}+r^{2}}}=\frac{\sigma}{2 \varepsilon_{0}} \frac{r d r}{\sqrt{H^{2}+r^{2}}} \end{aligned} $$
$\therefore$ Potential due to the complete disc
$$ \begin{aligned} V_{p} & =\int_{r=0}^{r=a} d V \\ & =\frac{\sigma}{2 \varepsilon_{0}} \int_{r=0}^{r=a} \frac{r d r}{\sqrt{H^{2}+r^{2}}} \\ V_{p} & =\frac{\sigma}{2 \varepsilon_{0}}\left[\sqrt{a^{2}+H^{2}}-H\right] \end{aligned} $$
Potential at centre, $(O)$ will be
$$ V_{O}=\frac{\sigma a}{2 \varepsilon_{0}} \quad H=0 $$
(a) Particle is released from $P$ and it just reaches point $O$. Therefore, from conservation of mechanical energy
Decrease in gravitational potential energy $=$ Increase in electrostatic potential energy
$$ \left(\Delta \mathrm{KE}=0 \text { because } K_{i}=K_{f}=0\right) $$
$$ \begin{aligned} & \therefore m g H=q\left[V_{O}-V_{p}\right] \\ & \text { or } g H=\frac{q}{m} \quad \frac{\sigma}{2 \varepsilon_{0}}\left[a-\sqrt{a^{2}+H^{2}}+H\right] \\ & \frac{q}{m}=\frac{4 \varepsilon_{0} g}{\sigma} \\ & \therefore \quad \frac{q \sigma}{2 \varepsilon_{0} m}=2 g \end{aligned} $$
Substituting in Eq. (i), we get
$$ \begin{aligned} & & g H & =2 g\left[a+H-\sqrt{a^{2}+H^{2}}\right] \\ & \text { or } & \frac{H}{2} & =(a+H)-\sqrt{a^{2}+H^{2}} \\ & \text { or } & \sqrt{a^{2}+H^{2}} & =a+\frac{H}{2} \\ & \text { or } & a^{2}+H^{2} & =a^{2}+\frac{H^{2}}{4}+a H \\ & \text { or } & \frac{3}{4} H^{2} & =a H \\ & \text { or } & H & =\frac{4}{3} a \\ & \text { and } & H & =0 \\ \therefore & & H & =(4 / 3) a \end{aligned} $$
(b) Potential energy of the particle at height $H=$ Electrostatic potential energy + gravitational potential energy
$$ \therefore \quad U=q V+m g H $$
Here $V=$ Potential at height $H$
$$ U=\frac{\sigma q}{2 \varepsilon_{0}}\left[\sqrt{a^{2}+H^{2}}-H\right]+m g H $$
At equilibrium position $F=\frac{-d U}{d H}=0$
Differentiating Eq. (ii) w.r.t. $H$
$$ \text { or } \begin{aligned} m g+\sigma \frac{q}{2 \varepsilon_{0}} \frac{1}{2}(2 H) \frac{1}{\sqrt{a^{2}+H^{2}}}-1 & =0 \\ & \because \frac{\sigma q}{2 \varepsilon_{0}}=2 m g \end{aligned} $$
$\therefore \quad m g+2 m g \frac{H}{\sqrt{a^{2}+H^{2}}}-1=0$
or $\quad 1+\frac{2 H}{\sqrt{a^{2}+H^{2}}}-2=0$
or $\frac{2 H}{\sqrt{a^{2}+H^{2}}}=1$ or $\frac{H^{2}}{a^{2}+H^{2}}=\frac{1}{4}$
or $\quad 3 H^{2}=a^{2}$ or $H=\frac{a}{\sqrt{3}}$
From Eq. (ii), we can write
$$ U-H \text { equation as } $$
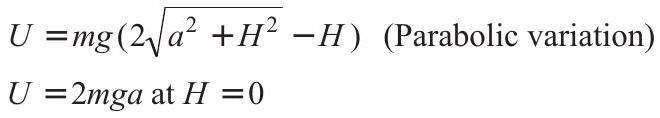
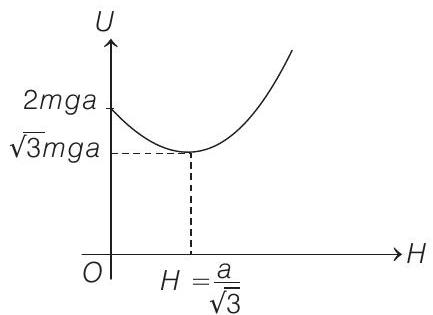
and $U=U_{\min }=\sqrt{3} m g a$ at $H=\frac{a}{\sqrt{3}}$
Therefore, $U-H$ graph will be as shown
Note that at $H=\frac{a}{\sqrt{3}}, U$ is minimum.
Therefore, $H=\frac{a}{\sqrt{3}}$ is stable equilibrium position.






