Electrostatics 6 Question 12
12. A part of circuit in a steady state along with the currents flowing in the branches, the values of resistances etc, is shown in the figure. Calculate the energy stored in the capacitor $C(4 \mu \mathrm{F})$.
$(1986,4 \mathrm{M})$
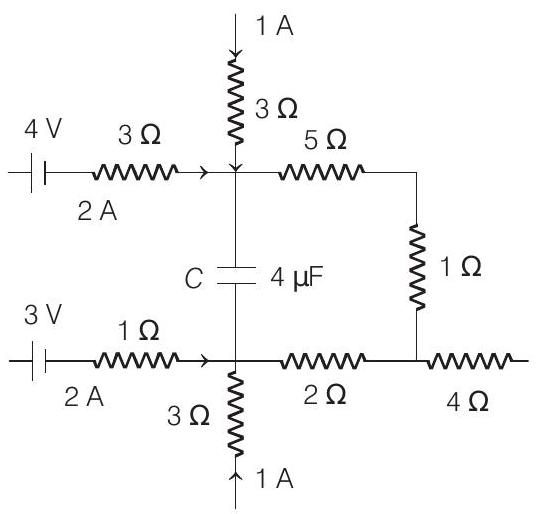
Show Answer
Answer:
Correct Answer: 12. 0.288 mJ
Solution:
- Using Kirchhoff’s first law at junctions $a$ and $b$, we have found the current in other wires of the circuit on which currents were not shown.
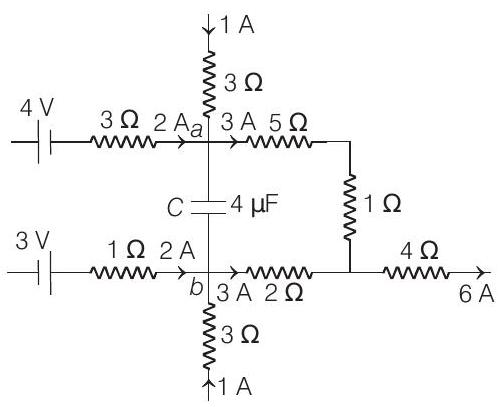
Now, to calculate the energy stored in the capacitor we will have to first find the potential difference $V_{a b}$ across it.
$$ \begin{array}{ll} \therefore & V_{a}-3 \times 5-3 \times 1+3 \times 2=V_{b} \\ \therefore & V_{a}-V_{b}=V_{a b}=12 \mathrm{~V} \\ \therefore & U=\frac{1}{2} C V_{a b}^{2}=\frac{1}{2}\left(4 \times 10^{-6}\right)(12)^{2} \mathrm{~J}=0.288 \mathrm{~mJ} \end{array} $$






