Electrostatics 5 Question 48
50. Two square metal plates of side $1 \mathrm{~m}$ are kept $0.01 \mathrm{~m}$ apart like a parallel plate capacitor in air in such a way that one of their edges is perpendicular to an oil surface in a tank filled with an insulating oil. The plates are connected to a battery of emf $500 \mathrm{~V}$. The plates are then lowered vertically into the oil at a speed of $0.001 \mathrm{~ms}^{-1}$. Calculate the current drawn from the battery during the process. (Dielectric constant of oil $=11$, $\left.\varepsilon_{0}=8.85 \times 10^{-12} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)$
(1994, 6M)
Show Answer
Answer:
Correct Answer: 50. $i = 4.43 \times {10}^{-9}A$
Solution:
- Let $a$ be the side of the square plate.
As shown in figure, $C_{1}$ and $C_{2}$ are in parallel. Therefore, total capacity of capacitors in the position shown is
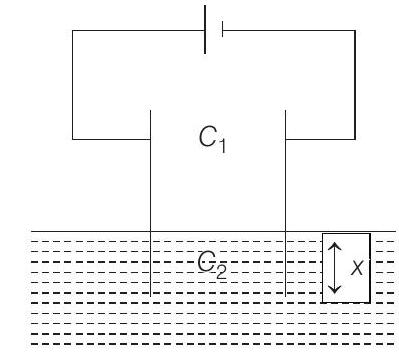
$$ \begin{aligned} & C=C_{1}+C_{2} \\ & C=\frac{\varepsilon_{0} a(a-x)}{d}+\frac{K \varepsilon_{0} a x}{d} \end{aligned} $$
$\therefore \quad q=C V=\frac{\varepsilon_{0} a V}{d}(a-x+K x)$
As plates are lowered in the oil, $C$ increases or charge stored will increase.
Therefore, $i=\frac{d q}{d t}=\frac{\varepsilon_{0} a V}{d}(K-1) \cdot \frac{d x}{d t}$
Substituting the values
$$ \begin{aligned} \varepsilon_{0} & =8.85 \times 10^{-12} \mathrm{C}^{2} / \mathrm{N}-\mathrm{m}^{2} \\ a & =1 \mathrm{~m}, V=500 \text { volt }, d=0.01 \mathrm{~m}, K=11 \end{aligned} $$
and $\frac{d x}{d t}=$ speed of plate $=0.001 \mathrm{~m} / \mathrm{s}$
We get current $i=\frac{\left(8.85 \times 10^{-12}\right)(1)(500)(11-1)(0.001)}{(0.01)}$
$$ i=4.43 \times 10^{-9} \mathrm{~A} $$






