Electrostatics 5 Question 19
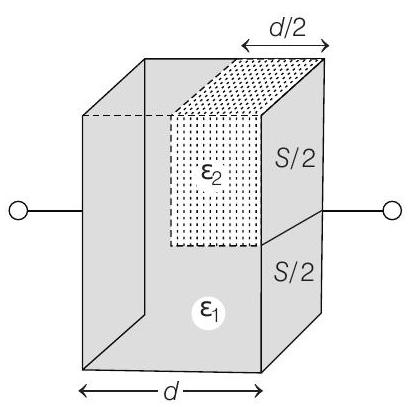
21. A parallel plate capacitor having plates of area $S$ and plate separation $d$, has capacitance $C_{1}$ in air. When two dielectrics of different relative permittivities $\left(\varepsilon_{1}=2\right.$ and $\left.\varepsilon_{2}=4\right)$ are introduced between the two plates as shown in the figure, the capacitance becomes $C_{2}$. The ratio $\frac{C_{2}}{C_{1}}$ is
(a) $\frac{6}{5}$
(b) $\frac{5}{3}$
(c) $\frac{7}{5}$
(d) $\frac{7}{3}$
(2015 Adv.)
Show Answer
Answer:
Correct Answer: 21. (d)
Solution:
$ C_{1}=\frac{\varepsilon_{0} s}{d}, C=\frac{2 \varepsilon_{0} \frac{s}{2}}{\frac{d}{2}}=\frac{2 \varepsilon_{0} s}{d} \Rightarrow C^{\prime}=\frac{4 \varepsilon_{0} \frac{s}{2}}{\frac{d}{2}}=\frac{4 \varepsilon_{0} s}{d} $
$ \begin{aligned} & \text { and } \quad C^{\prime \prime}=\frac{2 \varepsilon_{0} \frac{s}{2}}{d}=\frac{\varepsilon_{0} s}{d} \\ & C_{2}=\frac{C C^{\prime}}{C+C^{\prime}}+C^{\prime \prime}=\frac{4}{3} \frac{\varepsilon_{0} s}{d}+\frac{\varepsilon_{0} s}{d}=\frac{7}{3} \frac{\varepsilon_{0} s}{d} \frac{C_{2}}{C_{1}}=\frac{7}{3} \end{aligned} $
