Electrostatics 5 Question 18
20. A combination of capacitors is set-up as shown in the figure. The magnitude of the electric field, due to a point charge $Q$ (having a charge equal to the sum of the charges on the $4 \mu \mathrm{F}$ and $9 \mu \mathrm{F}$ capacitors), at a point distant $30 \mathrm{~m}$ from it, would equal to
(2016 Main)
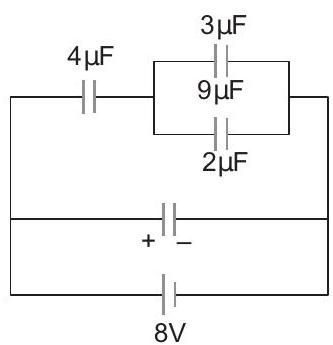
(a) $240 \mathrm{~N} / \mathrm{C}$
(b) $360 \mathrm{~N} / \mathrm{C}$
(c) $420 \mathrm{~N} / \mathrm{C}$
(d) $480 \mathrm{~N} / \mathrm{C}$
Show Answer
Answer:
Correct Answer: 20. (c)
Solution:
- $3 \mu \mathrm{F}$ and $9 \mu \mathrm{F}=12 \mu \mathrm{F}$
$ \begin{aligned} 4 \mu \mathrm{F} \text { and } 12 \mu \mathrm{F} & =\frac{4 \times 12}{4+12}=3 \mu \mathrm{F} \\ Q & =C V=3 \times 8=24 \mu \mathrm{C}(\text { on } 4 \mu \mathrm{F} \text { and } 3 \mu \mathrm{F}) \end{aligned} $
Now, this $24 \mu \mathrm{Cdistributes}$ in direct ratio of capacity between $3 \mu \mathrm{F}$ and $9 \mu \mathrm{F}$. Therefore,
$ \begin{aligned} Q_{9 \mu \mathrm{F}} & =18 \mu \mathrm{C} \\ \therefore Q_{4 \mu \mathrm{F}}+Q_{9 \mu \mathrm{F}}=24+18 & =42 \mu \mathrm{C}=Q \\ E & =\frac{k Q}{R^{2}}=\frac{9 \times 10^{9} \times 42 \times 10^{-6}}{30^{2}} \\ & =420 \mathrm{~N} / \mathrm{C} \end{aligned} $
