Electrostatics 5 Question 17
19. A capacitance of $2 \mu \mathbf{F}$ is required in an electrical circuit across a potential difference of $1 \mathrm{kV}$. A large number of $1 \mu \mathbf{F}$ capacitors are available which can withstand a potential difference of not more than $300 \mathrm{~V}$. The minimum number of capacitors required to achieve this is
(2017 Main)
(a) 16
(b) 24
(c) 32
(d) 2
Show Answer
Answer:
Correct Answer: 19. (c)
Solution:
- Let there are $n$ capacitors in a row with $m$ such rows in parallel.
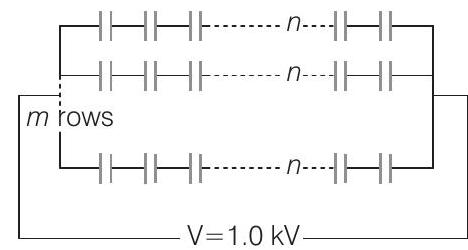
As voltage not to exceed $300 \mathrm{~V}$
$ \therefore \quad n \times 300>1000 $
[a voltage greater than $1 \mathrm{kV}$ to be withstand]
$ \begin{array}{lll} \Rightarrow & n>\frac{10}{3} \Rightarrow n=4 & \text { (or 3.33) } \\ \text { Also, } & C_{\mathbf{E q}}=\frac{m C}{n}=2 \mu \mathbf{F} & \\ \Rightarrow & \frac{m}{n}=2 \Rightarrow m=8 & {[\because C=1 \mu \mathbf{F}]} \end{array} $
So, total number of capacitors required
$ =m \times n=8 \times 4=32 $






