Electrostatics 5 Question 15
17. A parallel plate capacitor is made of two square plates of side ’ $a$ ’ separated by a distance $d(d«a)$. The lower triangular portions is filled with a dielectric of dielectric constant $k$, as shown in the figure. Capacitance of this capacitor is
(Main 2019, 9 Jan I)
(a) $\frac{K \varepsilon_0 a^2}{d} \ln \mathrm{K}$
(b) $\frac{K \varepsilon_0 a^2}{d(K-1)} \ln K$
(c) $\frac{K \varepsilon_0 a^2}{2 d(K+1)}$
(d) $\frac{1}{2} \cdot \frac{K \varepsilon_0 a^2}{d}$
Show Answer
Answer:
Correct Answer: 17. (b)
Solution:
- Let’s consider a strip of thickness ’ $d x$ ’ at a distance of ’ $x$ ’ from the left end as shown in the figure. From the figure, $\triangle A B C$ and $\triangle A D E$ are similar triangles,
$ \Rightarrow \quad \frac{y}{x}=\frac{d}{a} \Rightarrow y=\frac{d}{a} x $
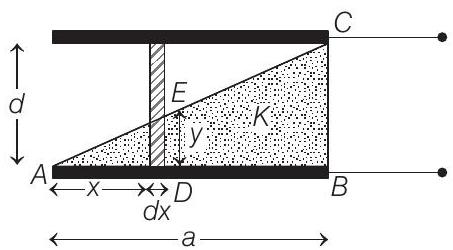
We know that, the capacitance of parallel plate capacitor,
$ \begin{aligned} C & =\frac{\varepsilon_{0} A}{d} \\ C_{1}=\frac{\varepsilon_{0}(a d x)}{(d-y)} \text { and } C_{2} & =\frac{K \varepsilon_{0}(a d x)}{y} \end{aligned} $
Here, two capacitor are placed in series with variable thickness, therefore
$ C_{\mathrm{eq}}=\frac{C_{1} C_{2}}{C_{1}+C_{2}} \Rightarrow C_{\mathrm{eq}}=\frac{K \varepsilon_{0} a d x}{K d+(1-K) y} $
Now, integrate it from 0 to $a$
$ C=\int_{0}^{a} \frac{K \varepsilon_{0} a d x}{K d+(1-K) y} $
Using Eq. (i), $y=\frac{d}{a} x$, we get
$ \begin{aligned} \quad C & =\varepsilon_{0} a \int_{0}^{a} \frac{d x}{d+\frac{1}{K}-1 \frac{d}{a} x} \\ \Rightarrow \quad C & =\frac{\varepsilon_{0} a}{\frac{1-K}{K} \frac{d}{a}} \ln \frac{1}{K} \\ \Rightarrow \quad C & =\frac{\varepsilon_{0} a^{2} K \ln K}{(K-1) d} \end{aligned} $
