Electrostatics 4 Question 1
1. A point dipole $\mathbf{p}=-p_{0} \hat{\mathbf{x}}$ is kept at the origin. The potential and electric field due to this dipole on the $Y$-axis at a distance $d$ are, respectively [Take, $V=0$ at infinity]
(a) $\frac{|\mathbf{p}|}{4 \pi \varepsilon_{0} d^{2}}, \frac{\mathbf{p}}{4 \pi \varepsilon_{0} d^{3}}$
(b) $0, \frac{-\mathbf{p}}{4 \pi \varepsilon_{0} d^{3}}$
(c) $0, \frac{\mathbf{p}}{4 \pi \varepsilon_{0} d^{3}}$
(d) $\frac{|\mathbf{p}|}{4 \pi \varepsilon_{0} d^{2}}, \frac{-\mathbf{p}}{4 \pi \varepsilon_{0} d^{3}}$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- The given problem can be shown as clearly potential difference at point $P$ due to dipole is
$ \begin{aligned} V & =V_{A P}+V_{B P}(\text { scalar addition }) \\ \Rightarrow \quad V & =\frac{k(-q)}{A P}+\frac{k(q)}{B P} \end{aligned} $
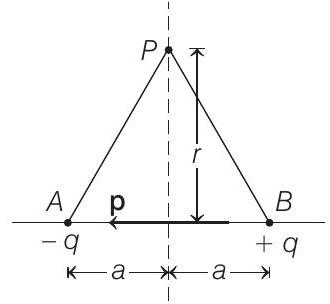
Here, $A P=B P=\sqrt{a^{2}+r^{2}}$
$\therefore \quad V=-\frac{k q}{\sqrt{a^{2}+r^{2}}}+\frac{k q}{\sqrt{a^{2}+r^{2}}}=0$
Now, electric field at any point on $Y$-axis, i.e. equatorial line of the dipole can be given by
$ \begin{array}{rlrl} & & \mathbf{E}=-\frac{k \mathbf{p}}{r^{3}} \\ \Rightarrow & & \mathbf{E}=-\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathbf{p}}{r^{3}} \\ \text { Given, } & r & =d \\ \therefore & & \mathbf{E} & =-\frac{1}{4 \pi \varepsilon_{0}} \frac{\mathbf{p}}{d^{3}} \end{array} $
From Eqs. (ii) and (iii), correct option is (b).
Alternate Solution
Electric field at any point at $\theta$ angle from axial line of dipole is given by
$ \mathbf{E}=-\frac{k \mathbf{p}}{r^{3}} \sqrt{3 \cos ^{2} \theta+1} $
Here, $\theta=90^{\circ} \Rightarrow \cos \theta=\cos 90^{\circ}=0$ and $r=d$
$ \therefore \quad \mathbf{E}=-\frac{k \mathbf{p}}{d^{3}}=-\frac{\mathbf{p}}{4 \pi \varepsilon_{0} d^{3}} $
