Electrostatics 3 Question 20
20. A charge $Q$ is distributed over two concentric hollow spheres of radii $r$ and $R(>r)$ such that the surface densities are equal. Find the potential at the common centre.
(1981, 3M)
Show Answer
Answer:
Correct Answer: 20. $\frac{Q(R+r)}{4 \pi \varepsilon_{0}\left(r^{2}+R^{2}\right)}$
Solution:
- Let $q_{1}$ and $q_{2}$ be the charges on them.
$ \begin{gathered} \sigma_{1}=\sigma_{2} \\ \therefore \quad \frac{q_{1}}{4 \pi r^{2}}=\frac{q_{2}}{4 \pi R^{2}} \Rightarrow \frac{q_{1}}{q_{2}}=\frac{r^{2}}{R^{2}} \end{gathered} $
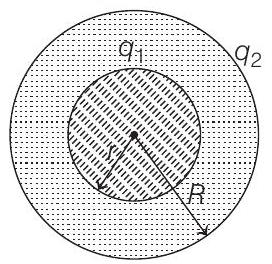
i.e., charge on them is distributed in above ratio.
or $q_{1}=\frac{r^{2}}{r^{2}+R^{2}} Q$ and $q_{2}=\frac{R^{2}}{r^{2}+R^{2}} Q$
Potential at centre $V=$ potential due to $q_{1}+$
or $\quad V=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{1}}{r}+\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q_{2}}{R}$
potential due to $q_{2}$
$ =\frac{Q(R+r)}{4 \pi \varepsilon_{0}\left(r^{2}+R^{2}\right)} $
