Electrostatics 3 Question 1
1. Shown in the figure is a shell made of a conductor. It has inner radius $a$ and outer radius $b$ and carries charge $Q$. At its centre is a dipole $\mathbf{p}$ as shown.
In this case,
(Main 2019, 12 April I)
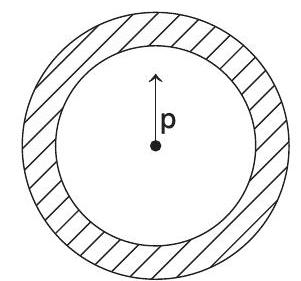
(a) surface charge density on the inner surface is uniform and
$$ \text { equal to } \frac{\frac{Q}{2}}{4 \pi a^{2}} $$
(b) electric field outside the shell is the same as that of a point charge at the centre of the shell
(c) surface charge density on the outer surface depends on $|\mathbf{p}|$
(d) surface charge density on the inner surface of the shell is zero everywhere
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Electric charge distribution at inner and outer surface of spherical shell due to the electric dipole can be shown as below
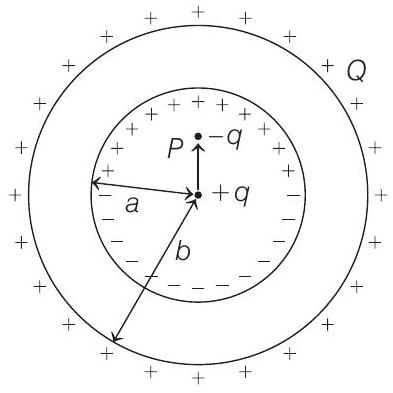
Here, we need to consider two different factors
(i) charge on the spherical shell is $+Q$ which will be distributed on its outer surface as shown in figure.
(ii) Electric dipole will create non-uniform electric field inside the shell which will distribute the charges on inner surface as shown in figure. But its net contribution to the outer side of the shell will be zero as net charge of a dipole is zero.
$\therefore$ Net charge on outer surface of shell will be $+Q$.
Hence, using (ii), option (a) is incorrect as field inside shell is not uniform. Option (b) is correct, as net charge on outer surface is $+Q$ even in the presence of dipole.
Option (c) is incorrect, as surface charge density at outer surface is uniform $=\frac{Q}{A}=\frac{Q}{4 \pi b^{2}}$.
Option (d) is incorrect, as surface charge density at inner surface is non-zero.
So, option (b) is correct.
Alternate Solution Using Gauss’ law at outer surface, let charge on dipole is $q$,
$$ \begin{aligned} \varphi & =\frac{\Sigma q}{\varepsilon _0}=E \cdot A \text { or } E=\frac{1}{A \varepsilon _0} \Sigma q \\ & =\frac{(+Q+q-q)}{A \varepsilon _0}=\frac{Q}{A \varepsilon _0}=\frac{\sigma}{\varepsilon _0}=\text { constant } \end{aligned} $$






