Electrostatics 2 Question 29
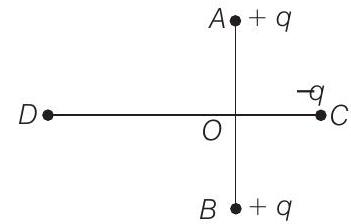
30. Two fixed, equal, positive charges, each of magnitude $q=5 \times 10^{-5} \mathrm{C}$ are located at points $A$ and $B$ separated by a distance of $6 \mathrm{~m}$. An equal and opposite charge moves towards them along the line $C O D$, the perpendicular bisector of the line $A B$. The moving charge, when reaches the point $C$ at a distance of $4 \mathrm{~m}$ from $O$, has a kinetic energy of $4 \mathrm{~J}$. Calculate the distance of the farthest point $D$ which the negative charge will reach before returning towards $C$.
$(1985,6 M)$
Show Answer
Answer:
Correct Answer: 30. Maximum distance from O = 8.48 m
Solution:
- Equating the energy of $(-q)$ at $C$ and $D$
$ \text { Here, } \begin{aligned} K_{C}+U_{C} & =K_{D}+U_{D} \\ K_{C} & =4 \mathrm{~J} \\ U_{C} & =2 \frac{1}{4 \pi \varepsilon_{0}} \frac{(q)(-q)}{A C} \\ & =\frac{-2 \times 9 \times 10^{9} \times\left(5 \times 10^{-5}\right)^{2}}{5}=-9 \mathrm{~J} \end{aligned} $
$ \begin{aligned} & K_{D}=0 \\ & \text { and } \end{aligned} $
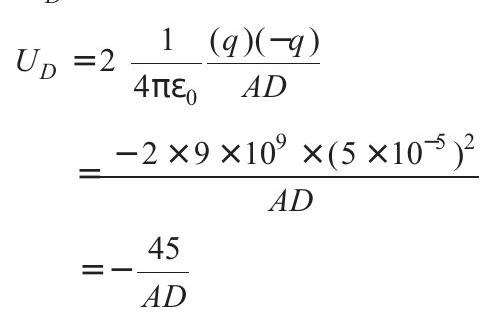
Substituting these values in Eq. (i)
$ \begin{aligned} \quad 4-9 & =0-\frac{45}{A D} \\ \therefore \quad \quad A D & =9 \mathrm{~m} \\ \therefore \quad O D & =\sqrt{A D^{2}-O A^{2}} \\ & =\sqrt{(9)^{2}-(3)^{2}} \\ & =\sqrt{81-9}=8.48 \mathrm{~m} \end{aligned} $






