Electrostatics 1 Question 3
3. Two point charges $q_{1}(\sqrt{10} \mu \mathrm{C})$ and $q_{2}(-25 \mu \mathrm{C})$ are placed on the $x$-axis at $x=1 \mathrm{~m}$ and $x=4 \mathrm{~m}$, respectively. The electric field (in V/m) at a point $y=3 \mathrm{~m}$ on $Y$-axis is
(Main 2019, 9 Jan II)
(Take, $\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} \mathrm{~N}-\mathrm{m}^{2} \mathrm{C}^{-2}$)
(a) $(63 \hat{\mathbf{i}}-27 \hat{\mathbf{j}}) \times 10^{2}$
(b) $(81 \hat{\mathbf{i}}-81 \hat{\mathbf{j}}) \times 10^{2}$
(c) $(-81 \hat{\mathbf{i}}+81 \hat{\mathbf{j}}) \times 10^{2}$
(d) $(-63 \hat{\mathbf{i}}+27 \hat{\mathbf{j}}) \times 10^{2}$
Show Answer
Answer:
Correct Answer: 3. (a)
Solution:
- Here, $q_{1}=\sqrt{10} \mu \mathrm{C}=\sqrt{10} \times 10^{-6} \mathrm{C}$
$q_{2}=-25 \mu \mathrm{C}=-25 \times 10^{-6} \mathrm{C}$
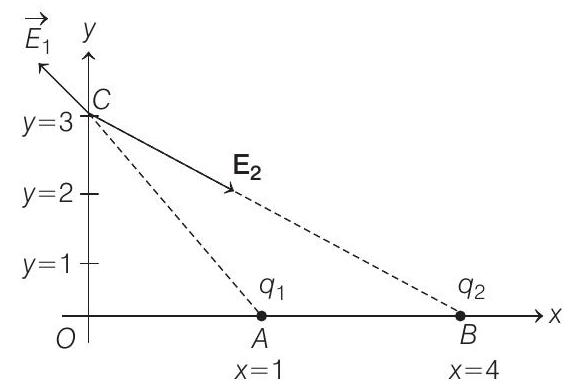
Let $\mathbf{E} _ 1$ and $\mathbf{E} _ 2$ are the values of electric field due to $q _ 1$ and $q _ 2$ respectively.
$$ \begin{aligned} \text { Here, } E _ 1 & =\frac{1}{4 \pi \varepsilon _ 0} \cdot \frac{q _ 1}{A C^{2}}=\frac{1}{4 \pi \varepsilon _ 0} \times \frac{\sqrt{10} \times 10^{-6}}{\left(1^{2}+3^{2}\right)} \\ & =9 \times 10^{9} \times \sqrt{10} \times 10^{-7} \\ & =9 \sqrt{10} \times 10^{2} \\ \therefore \quad \mathbf{E} _ 1 & =9 \sqrt{10} \times 10^{2}\left[\cos \theta _ 1(\hat{\mathbf{i}})+\sin \theta _ 1 \hat{\mathbf{j}}\right] \end{aligned} $$
From $\triangle O A C$,
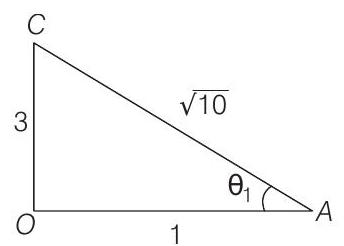
$$ \begin{aligned} & \sin \theta _ 1=\frac{3}{\sqrt{10}} \text { and } \cos \theta _ 1=\frac{1}{\sqrt{10}} \\ & \therefore E _ 1=9 \sqrt{10} \times 10^{2} \frac{1}{\sqrt{10}}(\hat{\mathbf{i}})+\frac{3}{\sqrt{10}} \hat{\mathbf{j}} \\ &=9 \times 10^{2}[\hat{\mathbf{i}}+3 \hat{\mathbf{j}}] \\ &=(-\hat{\mathbf{i}}+27 \hat{\mathbf{j}}) \times 10^{2} \mathrm{~V} / \mathrm{m} \end{aligned} $$
and $E _ 2=\frac{1}{4 \pi \varepsilon _ 0} \cdot \frac{-25 \times 10^{-6}}{\left(4^{2}+3^{2}\right)}=9 \times 10^{3} \mathrm{~V} / \mathrm{m}$
From $\triangle O B C$,
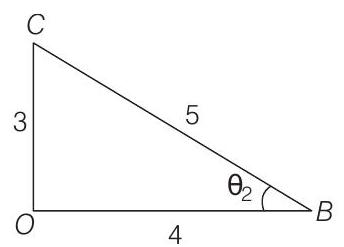
$$ \begin{aligned} & \sin \theta _ 2=\frac{3}{5} \\ & \cos \theta _ 2=\frac{4}{5} \\ \therefore \quad & \mathbf{E} _ 2=9 \times 10^{3}\left[\cos \theta _ 2 \hat{\mathbf{i}}-\sin \theta _ 2 \hat{\mathbf{j}}\right] \\ & \mathbf{E} _ 2=9 \times 10^{3} \frac{4}{5} \hat{\mathbf{i}}-\frac{3}{5} \hat{\mathbf{j}}=(72 \hat{\mathbf{i}}-54 \hat{\mathbf{j}}) \times 10^{2} \\ \therefore \quad & \mathbf{E}=\mathbf{E} _ 1+\mathbf{E} _ 2=(63 \hat{\mathbf{i}}-27 \hat{\mathbf{j}}) \times 10^{2} \mathrm{~V} / \mathrm{m} \end{aligned} $$






