Electrostatics 1 Question 22
23. Three particles, each of mass $1 \mathrm{~g}$ and carrying a charge $q$, are suspended from a common point by insulated massless strings, each $100 \mathrm{~cm}$ long. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side length $3 \mathrm{~cm}$, calculate the charge $q$ on each particle.
(Take $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ).
(1988, 5M)
Show Answer
Answer:
Correct Answer: 23. $3.17 \times 10^{-9} \mathrm{C}$
Solution:
$F$ is the resultant of electrostatic forces between two charges.
$$ \begin{aligned} F & =2 F_{e} \cos 30^{\circ} \\ & =2 \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q^{2}}{a^{2}} \frac{\sqrt{3}}{2} \\ & =\frac{2 \times 10^{9} \times 9 \times q^{2} \times \sqrt{3}}{\left(3 \times 10^{-2}\right)^{2} \times 2} \\ & =\sqrt{3} \times 10^{13} q^{2} \end{aligned} $$
$\theta$ is the angle of string with horizontal in equilibrium,
$$ \begin{aligned} & \cos \theta=\frac{r}{l}=\frac{(a / 2) \sec 30^{\circ}}{l}=\frac{a}{\sqrt{3} l}=\frac{3}{100 \sqrt{3}} \\ & \therefore \quad \theta \approx 89^{\circ} \end{aligned} $$
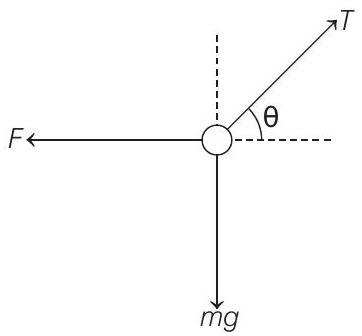
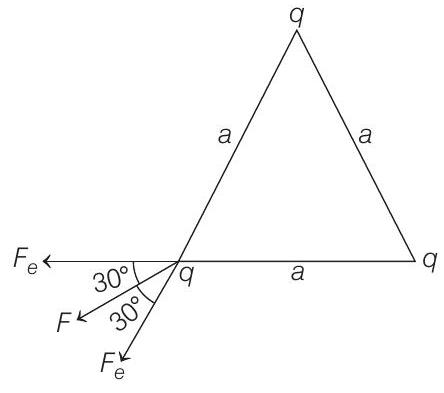
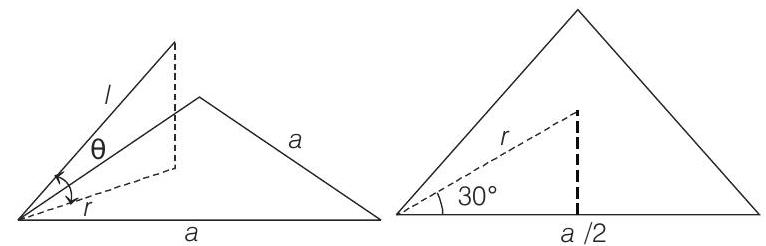
Now, the particle is in equilibrium under three concurrent forces, $F, T$ and $m g$. Therefore, applying Lami’s theorem
or
$$ \frac{F}{\sin \left(90^{\circ}+\theta\right)}=\frac{m g}{\sin \left(180^{\circ}-\theta\right)} $$
or
$$ \sqrt{3} \times 10^{13} q^{2}=\left(1 \times 10^{-3}\right)(10) \cot 89^{\circ} $$
Solving this equation, we get
$$ q=0.317 \times 10^{-8} \mathrm{C} \text { or } q=3.17 \times 10^{-9} \mathrm{C} $$
