Electrostatics 1 Question 2
2. Four point charges $-q,+q,+q$ and $-q$ are placed on $Y$-axis at $y=-2 d, y=-d, y=+d$ and $y=+2 d$, respectively. The magnitude of the electric field $E$ at a point on the $X$-axis at $x=D$, with $D \gg d$, will behave as
(Main 2019, 9 April II)
(a) $E \propto \frac{1}{D}$
(b) $E \propto \frac{1}{D^{3}}$
(c) $E \propto \frac{1}{D^{2}}$
(d) $E \propto \frac{1}{D^{4}}$
Show Answer
Answer:
Correct Answer: 2. (d)
Solution:
- Given charge distribution is as shown below
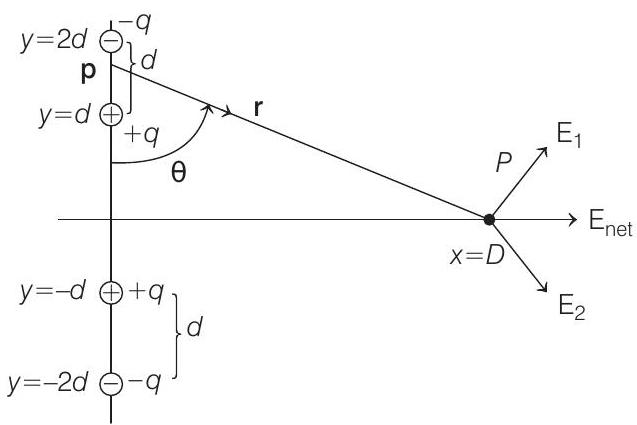
So, we can view above point charges as combination of pair of dipoles or a quadrupole.
By symmetry, the field components parallel to quadrupole cancels and the resultant perpendicular field is
$$ \begin{aligned} E & =\frac{2 q}{4 \pi \varepsilon _0} \frac{1}{D^{2}}-\frac{D}{\left(D^{2}+d^{2}\right)^{3 / 2}} \\ & =\frac{2 q}{4 \pi \varepsilon _0 D^{2}} 1-1+\frac{d^{2}}{D^{2}} \end{aligned} $$
As, $1+{\frac{d^{2}}{D^{2}}}^{-\frac{3}{2}} \approx 1-\frac{3}{2} \frac{d^{2}}{D^{2}}$ (using binomial expansion)
We have, $\quad E=\frac{3 q d^{2}}{4 \pi \varepsilon _0 D^{4}}$
$\therefore \quad E \propto \frac{1}{D^{4}}$
NOTE Dependence of field for a point charge is
$$ E \propto \frac{1}{r^{2}} $$
For a dipole, it is $E \propto \frac{1}{r^{3}}$
For a quadrupole, it is $E \propto \frac{1}{r^{4}} \ldots$. etc.
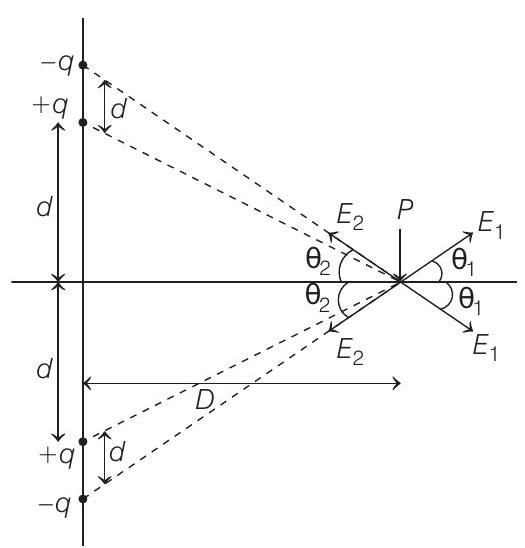
Alternate Solution The given distribution of charges can be shown as the figure below
Electric field at point $P$,
$E=E _1 \cos \theta _1+E _1 \cos \theta _1-E _2 \cos \theta _2-E _2 \cos \theta _2$
$=2 E _1 \cos \theta _1-2 E _2 \cos \theta _2$
$=\frac{2 k q}{\left(d^{2}+D^{2}\right)} \cos \theta _1-\frac{2 k q}{(2 d)^{2}+D^{2}} \cos \theta _2$
As, $\cos \theta _1=\frac{D}{\left(d^{2}+D^{2}\right)^{1 / 2}}$
Similarly, $\cos \theta _2=\frac{D}{\left[(2 d)^{2}+D^{2}\right]^{1 / 2}}$
$$ \begin{aligned} & =2 k q D\left[\left(d^{2}+D^{2}\right]^{-3 / 2}-\left(4 d^{2}+D^{2}\right)^{-3 / 2}\right] \\ & =\frac{2 k q D}{D^{3}} \quad 1+\frac{d^{2}}{D^{2}}-1+{\frac{4 d^{2}}{D^{2}}}^{-3 / 2} \end{aligned} $$
As $D»d$, then by applying binomial approximation, we get
$$ \begin{aligned} & =\frac{2 k q}{D^{2}} 1-\frac{3}{2} \frac{d^{2}}{D^{2}}-1-\frac{3}{2} \frac{4 d^{2}}{D^{2}} \\ & =\frac{2 k q}{D^{2}} \frac{9 d^{2}}{2 D^{2}}=\frac{9 k q d^{2}}{D^{4}} \\ \Rightarrow \quad E & \propto \frac{1}{D^{4}} \end{aligned} $$






