Electrostatics 1 Question 1
1. Let a total charge $2 Q$ be distributed in a sphere of radius $R$, with the charge density given by $\rho(r)=k r$, where $r$ is the distance from the centre. Two charges $A$ and $B$, of $-Q$ each, are placed on diametrically opposite points, at equal distance $a$, from the centre. If $A$ and $B$ do not experience any force, then
(Main 2019, 12 April II)
(a) $a=8^{-1 / 4} R$
(b) $a=\frac{3 R}{2^{1 / 4}}$
(c) $a=2^{-1 / 4} R$
(d) $a=R / \sqrt{3}$
Show Answer
Answer:
Correct Answer: 1. (a)
Solution:
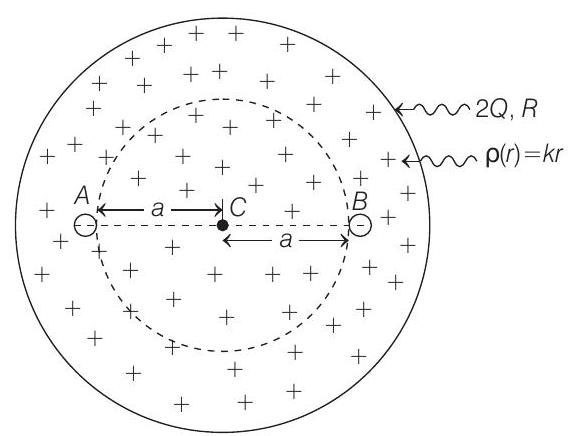
Key Idea Force on $A$ is zero only when repulsion of $A$ and $B=$ attraction of positive charge distribution of radius $a$ and charge $A$.
In given charge distribution, let $r$ is radius of a shell of thickness $d r$.
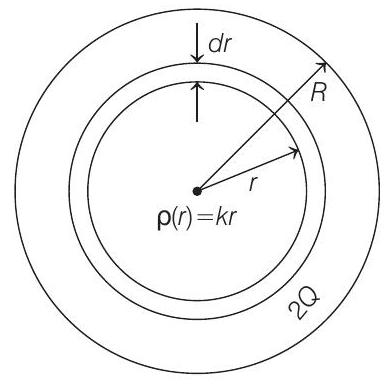
Charge $d Q$ present in shell of thickness $d r=$ Volume of shell $\times$ Volumetric charge density
$$ \begin{aligned} \Rightarrow \quad d Q & =\left(4 \pi r^{2} \times d r\right) \times(k r) \\ & =4 \pi k r^{3} d r \end{aligned} $$
Total charge in sphere is
$$ \begin{aligned} & 2 Q=\int_{0}^{R} d Q=\int_{0}^{R} 4 \pi k r^{3} d r \\ & \Rightarrow \quad 2 Q=4 \pi k{\frac{r^{4}}{4}}_{0}^{R} \Rightarrow k=\frac{2 Q}{\pi R^{4}} \end{aligned} $$
Now, using Gauss’ law, electric field on the surface of sphere of radius $a$ is
$$ \begin{array}{rlrl} E \int_{0}^{a} d A & =\frac{1}{\varepsilon_{0}} \cdot \int_{0}^{a}\left(k r 4 \pi r^{2} d r\right) \\ \Rightarrow \quad & E \cdot 4 \pi a^{2} & =\frac{1}{\varepsilon_{0}} \cdot 4 \pi k \frac{a^{4}}{4} \\ \Rightarrow & E & =\frac{k a^{2}}{4 \varepsilon_{0}}=\frac{2 Q a^{2}}{4 \pi \varepsilon_{0} R^{4}} \end{array} $$
Force of attraction on charge $A$ ( or $B$ ) due to this field is
$$ F_{1}=Q E=\frac{2 Q^{2} a^{2}}{4 \pi \varepsilon_{0} R^{4}} $$
Force of repulsion on charge $A$ due to $B$ is
$$ F_{2}=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q^{2}}{(2 a)^{2}}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q^{2}}{4 a^{2}} $$
If charge $A$ (or $B$ ) does not feel any force, then
$$ \begin{aligned} & F_{1}=F_{2} \\ & \Rightarrow \quad \frac{2 Q^{2} a^{2}}{4 \pi \varepsilon_{0} R^{4}}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q^{2}}{4 a^{2}} \\ & \Rightarrow \quad 8 a^{4}=R^{4} \Rightarrow a=8^{-1 / 4} R \end{aligned} $$






