Electromagnetic Induction and Alternating Current 7 Question 24
####27. A long circular tube of length $10 \mathrm{~m}$ and radius $0.3 \mathrm{~m}$ carries a current $I$ along its curved surface as shown. A wire-loop of resistance $0.005 \Omega$ and of radius $0.1 \mathrm{~m}$ is placed inside the tube with its axis coinciding with the axis of the tube.
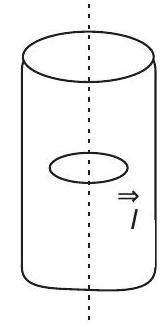
The current varies as $I=I_{0} \cos 300 t$ where $I_{0}$ is constant. If the magnetic moment of the loop is $N \mu_{0} I_{0} \sin (300 t)$, then $N$ is
(2011)
Show Answer
Answer:
Correct Answer: 27. 6
Solution:
- Take the circular tube as a long solenoid. The wires are closely wound. Magnetic field inside the solenoid is
$$ B=\mu_{0} n i $$
Here, $n=$ number of turns per unit length
$\therefore n i=$ current per unit length
In the given problem $n i=\frac{I}{L}$
$$ \therefore \quad B=\frac{\mu_{0} I}{L} $$
Flux passing through the circular coil is
$$ \varphi=B S=\frac{\mu_{0} I}{L}\left(\pi r^{2}\right) $$
Induced emf $\quad e=-\frac{d \varphi}{d t}=-\frac{\mu_{0} \pi r^{2}}{L} \cdot \frac{d I}{d t}$
Induced current, $i=\frac{e}{R}=-\frac{\mu_{0} \pi r^{2}}{L R} \cdot \frac{d I}{d t}$
Magnetic moment, $M=i A=i \pi r^{2}$
or
$$ M=-\frac{\mu_{0} \pi^{2} r^{4}}{L R} \cdot \frac{d I}{d t} $$
Given,
$$ I=I_{0} \cos (300 t) $$
$$ \therefore \quad \frac{d I}{d t}=-300 I_{0} \sin (300 t) $$
Substituting in Eq. (i), we get
$$ \begin{aligned} & M=\frac{\left.300 \pi^{2} r^{4}\right)}{L R} \mu_{0} I_{0} \sin (300 t) \\ \therefore \quad N & =\frac{300 \pi^{2} r^{4}}{L R} \end{aligned} $$
Substituting the values, we get
$$ N=\frac{300(22 / 7)^{2}(0.1)^{4}}{(10)(0.005)}=5.926 \text { or } N \simeq 6 $$






