Electromagnetic Induction and Alternating Current 7 Question 20
####20. The change in the magnetic dipole moment associated with the orbit, at the end of the time interval of the magnetic field change, is
(a) $\gamma B Q R^{2}$
(b) $-\mathrm{v} \frac{B Q R^{2}}{2}$
(c) $\gamma \frac{B Q R^{2}}{2}$
(d) $\gamma B Q R^{2}$
Show Answer
Answer:
Correct Answer: 20. (b)
Solution:
- $\frac{M}{L}=\frac{Q}{2 m}$
$\therefore \quad M=\frac{Q}{2 m} L \quad \Rightarrow \quad M \propto L$, where $\gamma=\frac{Q}{2 m}$
$$ =\frac{Q}{2 m} \quad(I \omega)=\frac{Q}{2 m} \quad\left(m R^{2} \omega\right)=\frac{Q \omega R^{2}}{2} $$
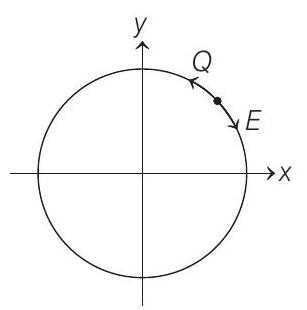
Induced electric field is opposite direction. Therefore,
$$ \begin{aligned} \omega^{\prime} & =\omega-\alpha t \\ \alpha & =\frac{\tau}{I}=\frac{(Q E) R}{m R^{2}} \\ & =\frac{(Q) \frac{B R}{2} R}{m R^{2}}=\frac{Q B}{2 m} \\ \therefore \quad \omega^{\prime} & =\omega-\frac{Q B}{2 m} \cdot 1=\omega-\frac{Q B}{2 m} \\ M_{f} & =\frac{Q \omega^{\prime} R^{2}}{2}=Q \omega-\frac{Q B}{2 m} \frac{R^{2}}{2} \end{aligned} $$
$$ \begin{array}{rlr} \therefore \Delta M & =M_{f}-M_{i}=-\frac{Q^{2} B R^{2}}{4 m} & \\ M & =-\gamma \frac{Q B R^{2}}{2} & (\because \gamma=\frac{Q}{2 m}) \end{array} $$






