Electromagnetic Induction and Alternating Current 4 Question 3
3. A
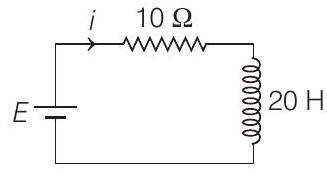 (Joule’s heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is
(Joule’s heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is
(Main 2019, 10 Jan I)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 3. (c)
Solution:
- Given circuit is a series
Now, energy stored in inductor is
where,
Given, rate of energy stored in inductor is equal to the rate of energy dissipation in resistor. So, after differentiating, we get
Taking log on both sides, we have






