Electromagnetic Induction and Alternating Current 4 Question 19
####19. An inductor of inductance $L=400 \mathrm{mH}$ and resistors of resistances $R_{1}=2 \Omega$ and $R_{2}=2 \Omega$ are connected to a battery of emf $E=12 \mathrm{~V}$ as shown in the figure. The internal resistance of the battery is negligible. The switch $S$ is closed at time $t=0$.
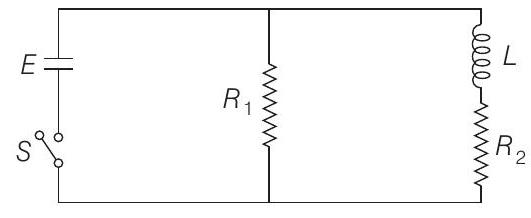
What is the potential drop across $L$ as a function of time? After the steady state is reached, the switch is opened. What is the direction and the magnitude of current through $R_{1}$ as a function of time?
$(2001,5 M)$
Show Answer
Answer:
Correct Answer: 19. $12 e^{-5 t} \mathrm{~V}, 6 e^{-10 t} \mathrm{~A} \text { (clockwise) }$
Solution:
- (a) Given, $R_{1}=R_{2}=2 \Omega, E=12 \mathrm{~V}$
and $L=400 \mathrm{mH}=0.4 \mathrm{H}$. Two parts of the circuit are in parallel with the applied battery. So, the upper circuit can be broken as
(a) 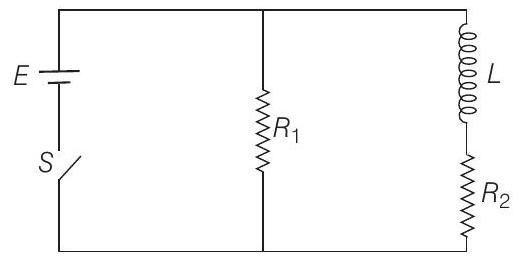
(b) 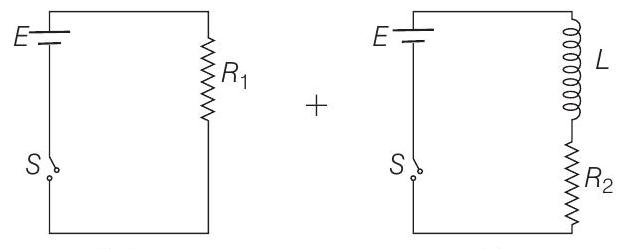
Now, refer Fig. (b)
This is a simple $L-R$ circuit, whose time constant
$$ \tau_{L}=L / R_{2}=\frac{0.4}{2}=0.2 \mathrm{~s} $$
and steady state current
$$ i_{0}=\frac{E}{R_{2}}=\frac{12}{2}=6 \mathrm{~A} $$
Therefore, if switch $S$ is closed at time $t=0$, then current in the circuit at any time $t$ will be given by
$$ \begin{aligned} i(t) & =i_{0}\left(1-e^{-t / \tau_{L}}\right) \\ i(t) & =6\left(1-e^{-t / 0.2}\right) \\ & =6\left(1-e^{-5 t}\right)=i \end{aligned} $$
Therefore, potential drop across $L$ at any time $t$ is
or
$$ \begin{aligned} & V=L \frac{d i}{d t}=L\left(30 e^{-5 t}\right)=(0.4)(30) e^{-5 t} \\ & V=12 e^{-5 t} \mathrm{~V} \end{aligned} $$
(b) The steady state current in $L$ or $R_{2}$ is
$$ i_{0}=6 \mathrm{~A} $$
Now, as soon as the switch is opened, current in $R_{1}$ is reduced to zero immediately. But in $L$ and $R_{2}$ it decreases exponentially. The situation is as follows
(c) 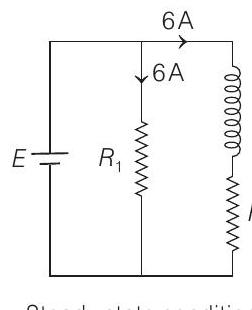
(d) 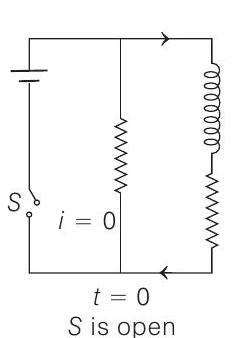
(e) 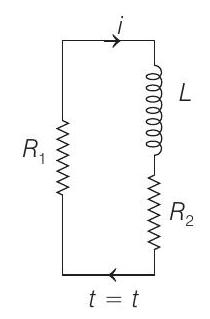
Refer figure (e) :
Time constant of this circuit would be
$$ \tau_{L}^{\prime}=\frac{L}{R_{1}+R_{2}}=\frac{0.4}{(2+2)}=0.1 \mathrm{~s} $$
$\therefore$ Current through $R_{1}$ at any time $t$ is
$$ i=i_{0} e^{-t / \tau_{L^{\prime}}}=6 e^{-t / 0.1} \text { or } i=6 e^{-10 t} \mathrm{~A} $$
Direction of current in $R_{1}$ is as shown in figure or clockwise.






