Electromagnetic Induction and Alternating Current 4 Question 17
####17. In an $L-R$ series circuit, a $V_{\uparrow}$ sinusoidal voltage $V=V_{0} \sin \omega t$ is applied. It is given that $L=35 \mathrm{mH}$, $R=11 \Omega, V_{\text {rms }}=220 \mathrm{~V}$,
$\omega / 2 \pi=50 \quad \mathrm{~Hz} \quad$ and $\pi=22 / 7$. Find the amplitude of current in the steady state and obtain the phase difference between the current and the voltage. Also plot the variation of current for one cycle on the given graph.
$(2004,4 M)$
Show Answer
Answer:
Correct Answer: 17. $20 A , \frac{\pi}{4}$
Solution:
- Inductive reactance,
$$ X_{L}=\omega L=(50)(2 \pi)\left(35 \times 10^{-3}\right) \approx 11 \Omega $$
Impedence, $Z=\sqrt{R^{2}+X_{L}^{2}}=\sqrt{(11)^{2}+(11)^{2}}=11 \sqrt{2} \Omega$
Given, $\quad V_{\mathrm{rms}}=220 \mathrm{~V}$
Hence, amplitude of voltage,
$$ V_{0}=\sqrt{2} V_{\mathrm{rms}}=220 \sqrt{2} \mathrm{~V} $$
$\therefore$ Amplitude of current, $i_{0}=\frac{V_{0}}{Z}=\frac{220 \sqrt{2}}{11 \sqrt{2}}$ or $i_{0}=20 \mathrm{~A}$
Phase difference, $\varphi=\tan ^{-1} \frac{X_{L}}{R}=\tan ^{-1} \frac{11}{11}=\frac{\pi}{4}$
In $L-R$ circuit, voltage leads the current. Hence, instantaneous current in the circuit is
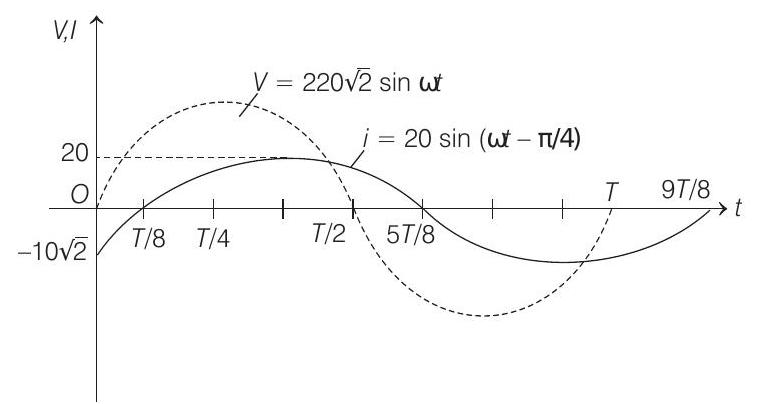
$$ i=(20 \mathrm{~A}) \sin (\omega t-\pi / 4) $$
Corresponding $i-t$ graph is shown in figure.
