Electromagnetic Induction and Alternating Current 4 Question 11
####11. In the figure below, the switches $S_{1}$ and $S_{2}$ are closed simultaneously at $t=0$ and a current starts to flow in the circuit. Both the batteries have the same magnitude of the electromotive force (emf) and the polarities are as indicated in the figure. Ignore mutual inductance between the inductors. The current $I$ in the middle wire reaches its maximum magnitude $I_{\max }$ at time $t=\tau$. Which of the following statements is (are) true?
(2018 Adv.)
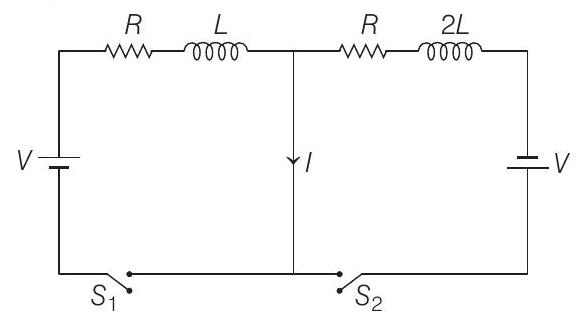
(a) $I_{\max }=\frac{V}{2 R}$
(b) $I_{\max }=\frac{V}{4 R}$
(c) $\tau=\frac{L}{R} \ln 2$
(d) $\tau=\frac{2 L}{R} \ln 2$
Show Answer
Answer:
Correct Answer: 11. (b, d)
Solution:
$$ I_{1}=\frac{V}{R} 1-e^{-\frac{t R}{L}} $$
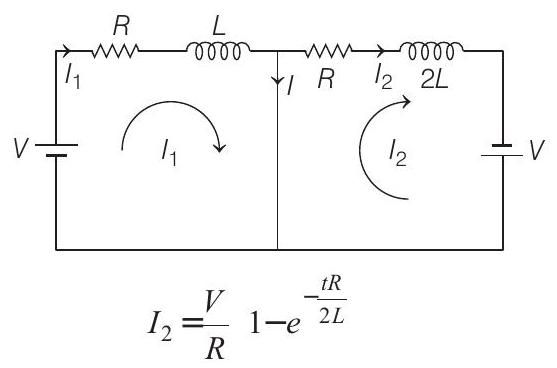
From principle of superposition,
$$ I=I_{1}-I_{2} \Rightarrow I=\frac{V}{R} e^{-\frac{t R}{2 L}} 1-e^{-\frac{t R}{2 L}} $$
$I$ is maximum when $\frac{d I}{d t}=0$, which gives
$$ e^{-\frac{t R}{2 L}}=\frac{1}{2} \text { or } t=\frac{2 L}{R} \ln 2 $$
Substituting this time in Eq. (i), we get $I_{\max }=\frac{V}{4 R}$






