Electromagnetic Induction and Alternating Current 1 Question 14
14. A metal bar $A B$ can slide on two parallel thick metallic rails separated by a distance $l$. A resistance $R$ and an inductance $L$ are connected to the rails as shown in the figure. A long straight
wire, carrying a constant current $I _0$ is placed in the plane of the rails as shown. The bar $A B$ is held at rest at a distance $x _0$ from the long wire. At $t=0$, it made to slide on the rails away from the wire. Answer the following questions.
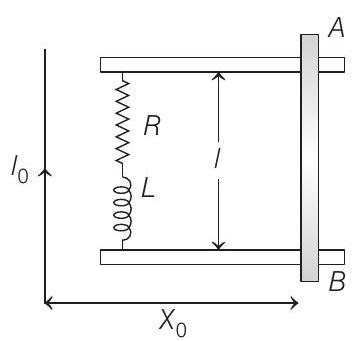
$(2002,5 M)$
(a) Find a relation among $i, \frac{d i}{d t}$ and $\frac{d \varphi}{d t}$, where $i$ is the current in the circuit and $\varphi$ is the flux of the magnetic field due to the long wire through the circuit.
(b) It is observed that at time $t=T$, the metal bar $A B$ is at a distance of $2 x _0$ from the long wire and the resistance $R$ carries a current $i _1$. Obtain an expression for the net charge that has flown through resistance $R$ from $t=0$ to $t=T$.
(c) The bar is suddenly stopped at time $T$. The current through resistance $R$ is found to be $i _1 / 4$ at time $2 T$. Find the value of $L / R$ in terms of the other given quantities.
Show Answer
Answer:
Correct Answer: 14. (a) $\frac{d \varphi}{d t}=i R+L \frac{d i}{d t}$ (b) $\frac{1}{R} \frac{\mu _0 I _0 l}{2 \pi}\left(\ln (2)-L i _1\right)$ (c) $\frac{T}{\ln (4)}$
Solution:
- (a) Applying Kirchhoff’s second law, we get
or
$$ \begin{aligned} & \frac{d \varphi}{d t}-i R-L \frac{d i}{d t}=0 \\ & \frac{d \varphi}{d t}=i R+L \frac{d i}{d t} \end{aligned} $$
This is the desired relation between $i, \frac{d i}{d t}$ and $\frac{d \varphi}{d t}$.
(b) Eq. (i) can be written as
$$ d \varphi=i R d t+L d i $$
Integrating, we get
$$ \begin{aligned} \Delta \varphi & =R \Delta q+L i _1 \\ \Delta q & =\frac{\Delta \varphi}{R}-\frac{L i _1}{R} \end{aligned} $$
$$ \text { Here, } \Delta \varphi=\varphi _f-\varphi _i=\int _{x=2 x _0}^{x=x _0} \frac{\mu _0}{2 \pi} \frac{I _0}{x} l d x=\frac{\mu _0 I _0 l}{2 \pi} \ln $$
So, from Eq. (ii) charge flown through the resistance upto time $t=T$, when current $i _1$, is
$$ \Delta q=\frac{1}{R} \frac{\mu _0 I _0 l}{2 \pi} \ln (2)-L i _1 $$
(c) This is the case of current decay in an $L-R$ circuit. Thus,
$$ i=i _0 e^{-t / \tau _L} $$
Here, $i=\frac{i _1}{4}, i _0=i _1, t=(2 T-T)=T$ and $\tau _L=\frac{L}{R}$
Substituting these values in Eq. (iii), we get
$$ \tau _L=\frac{L}{R}=\frac{T}{\ln 4} $$






