Centre of Mass 4 Question 10
11. A uniform thin $\operatorname{rod}$ of mass $M$ and length $L$ is standing vertically along the $Y$-axis on a smooth horizontal surface, with its lower end at the origin $(0,0)$. A slight disturbance at $t=0$ causes the lower end to slip on the smooth surface along the positive $X$-axis, and the rod starts falling. $\quad(1993,1+5 M)$ (a) What is the path followed by the centre of mass of the rod during its fall?
(b) Find the equation of the trajectory of a point on the rod located at a distance $r$ from the lower end. What is the shape of the path of this point?
Show Answer
Answer:
Correct Answer: 11. (a) Straight line
(b) $\frac{x^{2}}{\frac{L}{2}-r}+\frac{y^{2}}{r^{2}}=1$, ellipse
Solution:
- (a) Since, only two forces are acting on the rod, its weight $M g$ (vertically downwards) and a normal reaction $N$ at point of contact $B$ (vertically upwards).
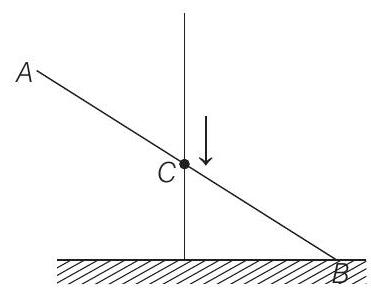
(a)
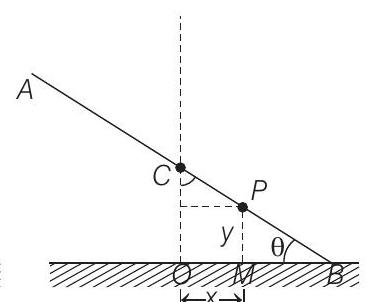
(b) No horizontal force is acting on the rod (surface is smooth).
Therefore, CM will fall vertically downwards towards negative $Y$-axis i.e. the path of $CM$ is a straight line.
(b) Refer figure (b). We have to find the trajectory of a point $P(x, y)$ at a distance $r$ from end $B$.
$$ \begin{array}{rlrl} & C B & =L / 2 \\ \therefore \quad & O B & =(L / 2) \cos \theta ; \\ \therefore & M B & =r \cos \theta \\ & x & =O B-M B \\ & =\cos \theta{(L / 2-r)} \\ \text { or } \quad & \cos \theta & =\frac{x}{{(L / 2)-r}} \end{array} $$
Similarly, $\quad y=r \sin \theta$
or
$$ \sin \theta=\frac{y}{r} $$
Squaring and adding Eqs. (i) and (ii), we get
$$ \begin{gathered} \sin ^{2} \theta+\cos ^{2} \theta=\frac{x^{2}}{{(L / 2)-r}^{2}}+\frac{y^{2}}{r^{2}} \\ \frac{x^{2}}{{(L / 2)-r}^{2}}+\frac{y^{2}}{r^{2}}=1 \end{gathered} $$
This is an equation of an ellipse. Hence, path of point $P$ is an ellipse whose equation is given by (iii).






