Centre of Mass 1 Question 15
15. A ball of mass $100 g$ is projected vertically upwards from the ground with a velocity of $49 m / s$. At the same time, another identical ball is dropped from a height of $98 m$ to fall freely along the same path as that followed by the first ball. After some time, the two balls collide and stick together and finally fall to the ground. Find the time of flight of the masses.
$(1985,8$ M)
Show Answer
Answer:
Correct Answer: 15. $6.53 s$
Solution:
- Both the balls are of equal masses. Therefore, their centre of mass is at height $98 / 2=49 m$ from ground. Acceleration of both the balls is $g$ downwards. Therefore, acceleration of their centre of mass is also $g$ downwards. Further, initially one ball has a velocity $49 m / s$.
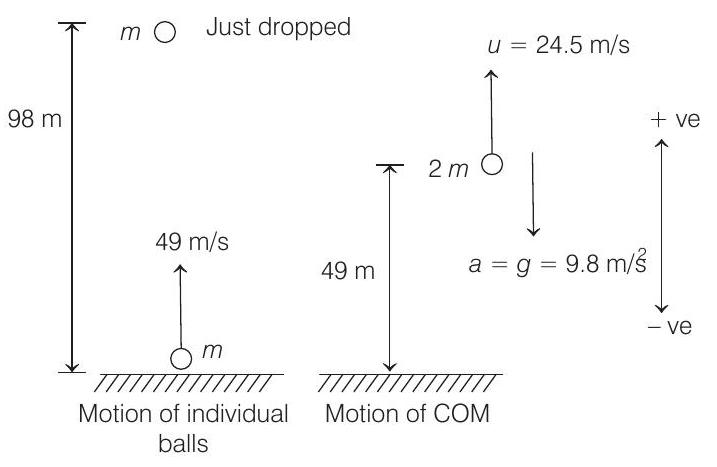
While the other is at rest. Therefore, initial velocity of their centre of mass is $49 / 2=24.5 m / s$ upwards. So, looking the motion of their centre of mass. Let it strikes after time $t$ with the ground. Putting the proper values with sign in equation.
$$ \begin{aligned} s & =u t+\frac{1}{2} a t^{2} \\ -49 & =24.5 t-4.9 t^{2} \\ \text { or } \quad t^{2}-5 t-10 & =0 \\ \text { or } \quad t & =\frac{5 \pm \sqrt{25+40}}{2} \end{aligned} $$
The positive value of $t$ from this equation comes out to be, $6.53 s$. Therefore, time of flight of the balls is $6.53 s$.






