SATHEE: Vectors 3 Question 19

Vectors 3 Question 19

19. Let $u = u_{1} \hat{i} + u_{2} \hat{j} + u_{3} \hat{k}$ be a unit vector in $R^{3}$ and $w = \frac{1}{\sqrt{6}} (\hat{i} + \hat{j} + 2 \hat{k})$ . Given that there exists a vector $v$ in $R^{3}$ , such that $| u + v | = 1$ and $w \cdot (u + v) = 1$ . Which of the following statement(s) is/are correct?

(a) There is exactly one choice for such $v$

(b) There are infinitely many choices for such $v$

(d) If $\hat{u}$ lies in the $X Y$ -plane, then $2 | u_{1} | = | u_{3} |$

Show Answer

Answer:

Correct Answer: 19. (b, c)

Solution:

Let $θ$ be the angle between $\hat{u}$ and $\vec{v}$ .

$\begin{array}{lll} ∴ & | u \times \vec{v} | = 1 \Rightarrow | u | \vec{v} ∣ \sin θ = 1 \\ ∴ & | \vec{v} | \sin θ = 1 & [∵ | u | = 1] \dots (i) \end{array}$

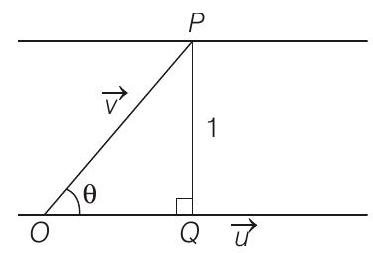
Clearly, there may be infinite vectors $\vec{O P} = \vec{v}$ , such that $P$ is always 1 unit distance from $\hat{u}$ .

$∴$ Option (b) is correct.

Again, let $ϕ$ be the angle between $w w$ and $u \times \vec{v}$ .

$\begin{aligned} ∴ w \cdot (u \times \vec{v}) = 1 \Rightarrow | w | | u \times \vec{v} | \cos ϕ = 1 \\ \Rightarrow \cos ϕ = 1 \Rightarrow ϕ = 0 \end{aligned}$

Thus,

$w = u \times \vec{v}$

Now, if $\hat{u}$ lies in $X Y$ -plane, then

$\begin{aligned} u \times \vec{v} = | \begin{array}{ccc} i & \hat{j} & k \\ u_{1} & u_{2} & 0 \\ v_{1} & v_{2} & v_{3} \end{array} | or u = u \hat{i} + u_{2} \hat{j} \\ ∴ & w = (u_{2} v_{3}) \hat{i} - (u_{1} v_{3}) \hat{j} + (u_{1} v_{2} - v_{1} u_{2}) \hat{k} \\ = \frac{1}{\sqrt{6}} (\hat{i} + \hat{j} + 2 \hat{k}) \\ ∴ & u_{2} v_{3} & = \frac{1}{\sqrt{6}}, u_{1} v_{3} = \frac{- 1}{\sqrt{6}} \\ \Rightarrow & \frac{u_{2} v_{3}}{u_{1} v_{3}} & = & - 1 or | u_{1} | = | u_{2} | \end{aligned}$

$∴$ Option (c) is correct.

Now, if $\hat{u}$ lies in $X Z$ -plane, then $u = u_{1} \hat{i} + u_{3} \hat{k}$

$\begin{aligned} ∴ u \times \vec{v} = | \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ u_{1} & 0 & u_{3} \\ v_{1} & v_{2} & v_{3} \end{array} | \\ \Rightarrow w = (- v_{2} u_{3}) \hat{i} - (u_{1} v_{3} - u_{3} v_{1}) \hat{j} + (u_{1} v_{2}) \hat{k} \\ \Rightarrow \hat{k} = \frac{1}{\sqrt{6}} (\hat{i} + \hat{j} + 2 \hat{k}) \\ \Rightarrow - v_{2} u_{3} = \frac{1}{\sqrt{6}} and u_{1} v_{2} = \frac{2}{\sqrt{6}} \\ ∴ | u_{2} | = 2 | u_{3} | \end{aligned}$

$∴$ Option $(d)$ is wrong.

Vectors 3 Question 19

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Vectors 3 Question 19

19. Let u=u1i^+u2j^+u3k^ be a unit vector in R3 and w=16(i^+j^+2k^). Given that there exists a vector v in R3, such that |u+v|=1 and w⋅(u+v)=1. Which of the following statement(s) is/are correct?

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu