Vectors 2 Question 10
10. If the vectors $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}$ and $\overrightarrow{\mathbf{c}}$ from the sides $B C, C A$ and $A B$ respectively of a $\triangle A B C$, then
(2000, 2M)
(a) $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{c}} \cdot \overrightarrow{\mathbf{a}}=0$
(b) $\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}}=\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{a}}$
(c) $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{c}}=\overrightarrow{\mathbf{c}} \cdot \overrightarrow{\mathbf{a}}$
(d) $\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{a}}=\overrightarrow{\mathbf{0}}$
Show Answer
Answer:
Correct Answer: 10. (b)
Solution:
- By triangle law, $\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}}=\overrightarrow{\mathbf{0}}$
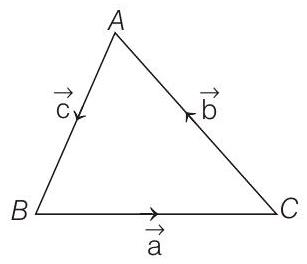
Taking cross product by $\overrightarrow{\mathbf{a}}, \overrightarrow{\mathbf{b}}, \overrightarrow{\mathbf{c}}$ respectively,
$ \overrightarrow{\mathbf{a}} \times(\overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}})=\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{0}}=\overrightarrow{\mathbf{0}} $
$\Rightarrow \quad \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{a}}+\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{c}}=\overrightarrow{\mathbf{a}} $
$\Rightarrow \quad \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{a}} \quad[\because \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{a}}=\overrightarrow{0}] $
$\text { Similarly, } \quad \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{a}} $
$\therefore \quad \overrightarrow{\mathbf{a}} \times \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{b}} \times \overrightarrow{\mathbf{c}}=\overrightarrow{\mathbf{c}} \times \overrightarrow{\mathbf{a}}$
