Vectors 1 Question 4
4. Let $\mathbf{a}=\hat{\mathbf{i}}+\hat{\mathbf{j}}+\sqrt{2} \hat{\mathbf{k}}, \mathbf{b}=b _1 \hat{\mathbf{i}}+b _2 \hat{\mathbf{j}}+\sqrt{2} \hat{\mathbf{k}} \quad$ and $\mathbf{c}=5 \hat{\mathbf{i}}+\hat{\mathbf{j}}+\sqrt{2} \hat{\mathbf{k}}$ be three vectors such that the projection vector of $\mathbf{b}$ on $\mathbf{a}$ is $\mathbf{a}$. If $\mathbf{a}+\mathbf{b}$ is perpendicular to $\mathbf{c}$, then $|\mathbf{b}|$ is equal to
(a) 6
(b) 4
(c) $\sqrt{22}$
(d) $\sqrt{32}$
Show Answer
Answer:
Correct Answer: 4. (b)
Solution:
- According to given information, we have the following figure.
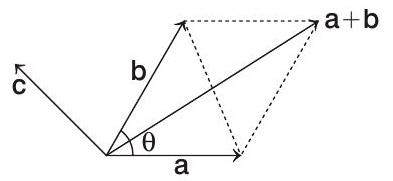
Clearly, projection of $b$ on $a=\frac{b \cdot a}{|a|}$
$ \begin{aligned} & =\frac{\left(b _1 \hat{i}+b _2 \hat{j}+\sqrt{2} \hat{k}\right)(\hat{i}+\hat{j}+\sqrt{2} \hat{k})}{\sqrt{1^{2}+1^{2}+(\sqrt{2})^{2}}} \\ & =\frac{b _1+b _2+2}{\sqrt{4}}=\frac{b _1+b _2+2}{2} \end{aligned} $
But projection of $b$ on $a=|a|$
$\therefore \frac{b _1+b _2+2}{2}=\sqrt{1^{2}+1^{2}+(\sqrt{2})^{2}}$
$\Rightarrow \frac{b _1+b _2+2}{2}=2 \Rightarrow b _1+b _2=2$
Now, $a+b=(\hat{i}+\hat{j}+\sqrt{2} \hat{k})+\left(b _1 \hat{i}+b _2 \hat{j}+\sqrt{2} \hat{k}\right)$
$ =\left(b _1+1\right) \hat{i}+\left(b _2+1\right) \hat{j}+2 \sqrt{2} \hat{k} $
$\because(a+b) \perp c$, therefore $(a+b) \cdot c=0$
$\Rightarrow {(b _1+1) \hat{i}+(b _2+1) \hat{j}+2 \sqrt{2} \hat{k}}(5 \hat{i}+\hat{j}+\sqrt{2} \hat{k})=0$
$\Rightarrow 5\left(b _1+1\right)+1\left(b _2+1\right)+2 \sqrt{2}(\sqrt{2})=0$
$\Rightarrow \quad 5 b _1+b _2=-10$
From Eqs. (i) and (ii), $b _1=-3$ and $b _2=5$
$\Rightarrow b=-3 \hat{i}+5 \hat{j}+\sqrt{2} \hat{k}$
$\Rightarrow|b|=\sqrt{(-3)^{2}+(5)^{2}+(\sqrt{2})^{2}}=\sqrt{36}=6$
