Vectors 1 Question 29
30. Let
(1988, 3M)
Show Answer
Answer:
Correct Answer: 30. (
Solution:
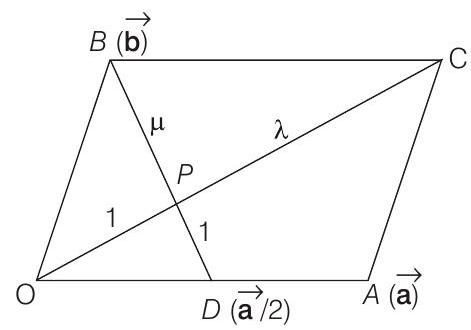
[along
[along
On solving, we get
Thus, required ratio is






