Vectors 1 Question 28
29. In a
Show Answer
Answer:
Correct Answer: 29. (
- Let
[since
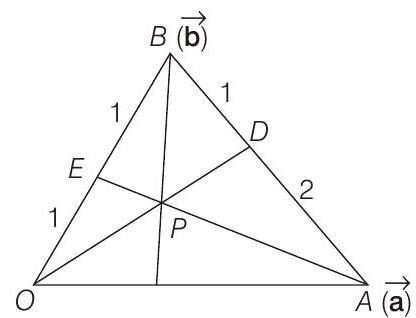
(since,
and equation of
If
Since,
From Eqs. (i) and (ii),






