Trigonometrical Equations 2 Question 4
4. Find all values of
(1996, 2M)
Show Answer
Answer:
Correct Answer: 4.
Solution:
- Given,
Put
NOTE
Curves
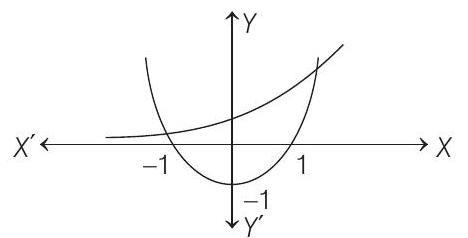
It is clear from the graph that two curves intersect at one point at
Therefore,






