Theory of Equations 5 Question 13
13. The function
(a) increasing in
(b) decreasing in
(c) increasing in
(d) decreasing in
Passage II
If a continuous function
(2007, 4M)
Show Answer
Answer:
Correct Answer: 13. (b)
Solution:
- As,
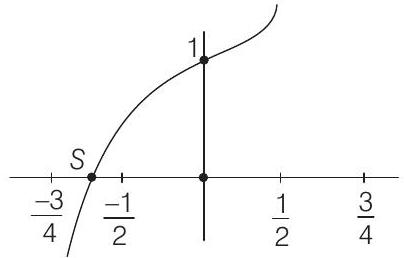
(a) increasing in
(b) decreasing in
(c) increasing in
(d) decreasing in
If a continuous function
(2007, 4M)
Correct Answer: 13. (b)
Solution:

© 2024 Copyright SATHEE
Powered by Prutor@IITK
Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓
I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".