Straight Line and Pair of Straight Lines 5 Question 1
1.
Let $P Q R$ be a right angled isosceles triangle, right angled at $P(2,1)$. If the equation of the line $Q R$ is $2 x+y=3$, then the equation representing the pair of lines $P Q$ and $P R$ is
$(1999,2 M)$
(a) $3 x^{2}-3 y^{2}+8 x y+20 x+10 y+25=0$
(b) $3 x^{2}-3 y^{2}+8 x y-20 x-10 y+25=0$
(c) $3 x^{2}-3 y^{2}+8 x y+10 x+15 y+20=0$
(d) $3 x^{2}-3 y^{2}-8 x y-10 x-15 y-20=0$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Let $S$ be the mid-point of $Q R$ and given $\triangle P Q R$ is an isosceles.
Therefore, $P S \perp Q R$ and $S$ is mid-point of hypotenuse, therefore $S$ is equidistant from $P, Q, R$.
$ \begin{array}{lc} \therefore & P S=Q S=R S \\ \text { Since, } & \angle P=90^{\circ} \text { and } \angle Q=\angle R \\ \text { But } & \angle P+\angle Q+\angle R=180^{\circ} \end{array} $
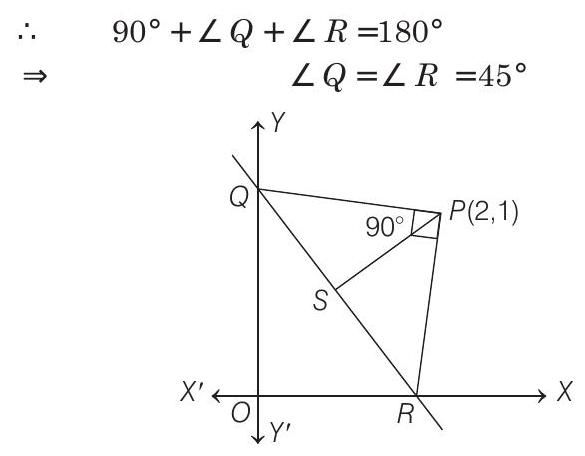
Now, slope of $Q R$ is -2 .
[given]
But $Q R \perp P S$.
$\therefore$ Slope of $P S$ is $1 / 2$.
Let $m$ be the slope of $P Q$.
$\therefore \quad \tan \left( \pm 45^{\circ}\right)=\frac{m-1 / 2}{1-m(-1 / 2)}$
$ \Rightarrow \quad \pm 1=\frac{2 m-1}{2+m} $
$\Rightarrow \quad m=3,-1 / 3$
$\therefore$ Equations of $P Q$ and $P R$ are
$ \begin{aligned} & y-1=3(x-2) \\ & \text { and } \quad y-1=-\frac{1}{3}(x-2) \\ & \text { or } \quad 3(y-1)+(x-2)=0 \end{aligned} $
Therefore, joint equation of $P Q$ and $P R$ is
$ [3(x-2)-(y-1)][(x-2)+3(y-1)]=0 $
$\Rightarrow \quad 3(x-2)^{2}-3(y-1)^{2}+8(x-2)(y-1)=0$
$\Rightarrow \quad 3 x^{2}-3 y^{2}+8 x y-20 x-10 y+25=0$
