Straight Line and Pair of Straight Lines 1 Question 60
60. Let
Show Answer
Solution:
- Let
Given,
Let
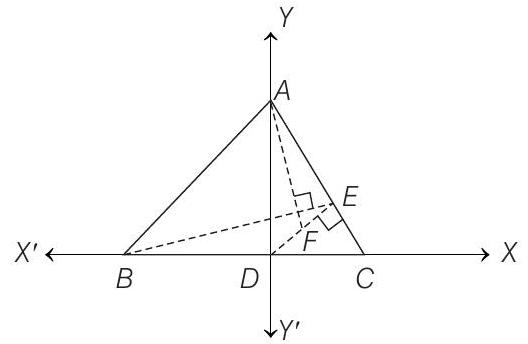
Then, equation of
and equation of
On solving, Eqs. (i) and (ii), we get the coordinates of point
Since,
and slope of
From Eqs. (iii) and (iv),






