Straight Line and Pair of Straight Lines 1 Question 24
24. The locus of the orthocentre of the triangle formed by the lines
(2009)
(a) a hyperbola
(b) a parabola
(c) an ellipse
(d) a straight line
Show Answer
Solution:
- Given, lines are
and
On solving Eqs. (i) and (ii), we get
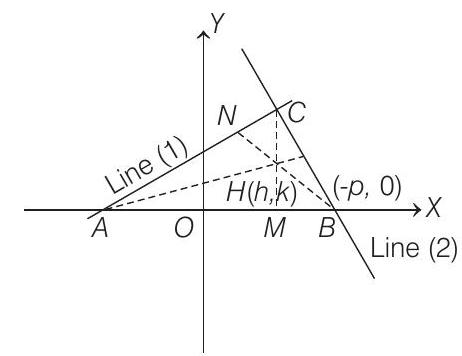
Let orthocentre of triangle be
On solving Eqs. (iii) and (iv), we get






